【笔记】基于图像的三维重建——三维重建基础与对极几何

本文主要关于深蓝学院系列课程——基于图像的三维重建的笔记。

课程链接 基于图像的三维重建

1、单视几何

1.1、无穷远点、无穷远线与无穷远面

无穷远点： 空间中平行线的交点。

无穷远线： 平行平面在无穷远处交于一条公共线。

无穷远面： 两条或多条无穷远直线的集合。

表示： 无穷远点与无穷远面表示如下（三维空间无穷远线较难表示，一般是两个平面的交线表示）：

$$无穷远点： \quad X_\infty=\begin{pmatrix}a\\b\\c\\0\end{pmatrix} \\ 无穷远面： \quad\Pi_\infty=\begin{pmatrix}0\\0\\0\\1\end{pmatrix}$$

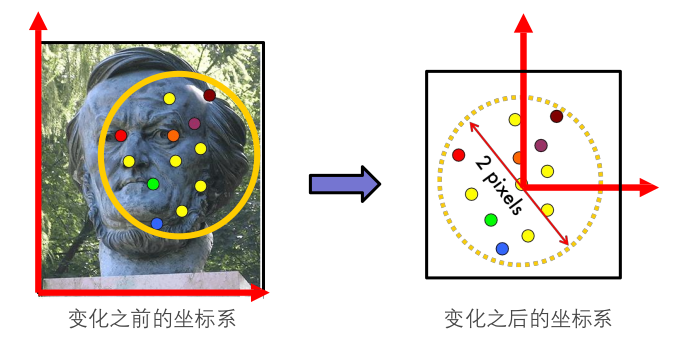
1.2、隐消点和隐消线

隐消点： 三维空间中无穷远点在图像平面上的投影点，其与直线方向满足如下关系：其中 $v$ 为隐消点， $d$ 为直线方向， $K$ 为相机投影矩阵。

$$v=Kd\quad\boxed{\Longrightarrow}\quad d=\frac{K^{-1}v}{||K^{-1}v||}$$

2D平面上的直线变换： 已知：直线 $l$ 和变换矩阵 $H$ ，求解变换后的直线 $l’$ ：

$${l^{\prime}=H^{-\mathrm{T}}l} \\ 隐消线l_{\infty}与其投影线有：\quad l_{h}=M^{-\mathrm{T}}l_{\infty}$$

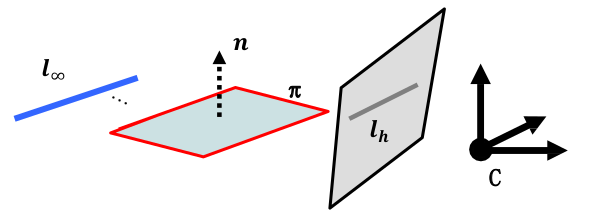
隐消线与平面法向量： 识别隐消线有助于重构。**图像中两条直线如果消失在隐消线上，则这两条线是3D空间中的平行线。

$${n=K^\mathrm{T}l_h}$$

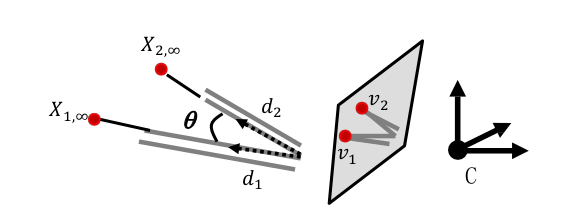
两组平行线的夹角与隐消点：

$${cos\theta}=\frac{d_1\cdot d_2}{|d_1||d_2|}=\frac{(K^{-1}v_1)^\mathrm{T}}{\sqrt{(K^{-1}v_1)^\mathrm{T}K^{-1}v_1}}\frac{K^{-1}v_2}{\sqrt{(K^{-1}v_2)^\mathrm{T}K^{-1}v_2}} \\ 令 W=K^{\mathrm{T}}K^{-1}=(KK^{\mathrm{T}})^{-1} \\ cos\theta = \frac{v_1^\mathrm{T}Wv_2}{\sqrt{v_1^\mathrm{T}Wv_1}\sqrt{v_2^\mathrm{T}Wv_2}}$$

$W$ 的性质：

1. $\boldsymbol{W}=\begin{pmatrix}W_1&W_2&W_4\\W_2&W_3&W_5\\W_4&W_5&W_6\end{pmatrix}$ 对称；
2. $W_2 = 0$ 为零倾斜投影；
3. $W_2=0; W_1 = W_3$ ，相机为方形像素；
4. $W$ 仅 5个 自由度。

总结：

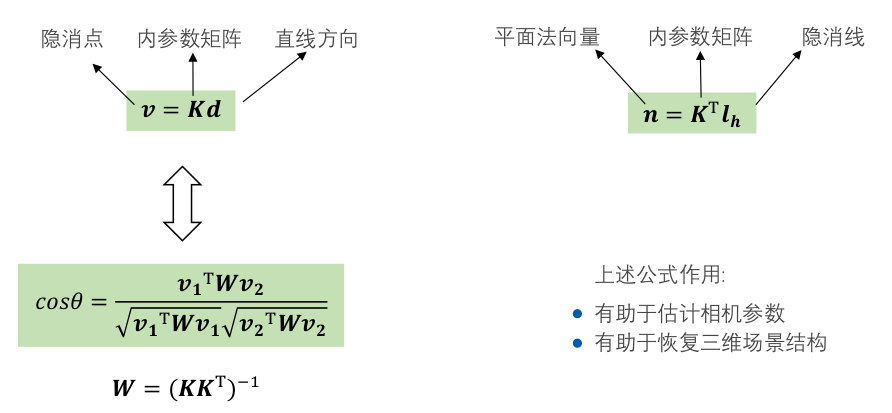
1.3、单视图标定

两个假设： 零倾斜；正方形像素。可以得到两个内参。

三个消隐点： 根据 两两垂直 的消隐点得到三条方程，求解剩下的内参：

$$\begin{cases}\boldsymbol{v_1}^\mathrm{T}\boldsymbol{Wv_2}=0\\\boldsymbol{v_1}^\mathrm{T}\boldsymbol{Wv_3}=0\\\boldsymbol{v_2}^\mathrm{T}\boldsymbol{Wv_3}=0&\end{cases}$$

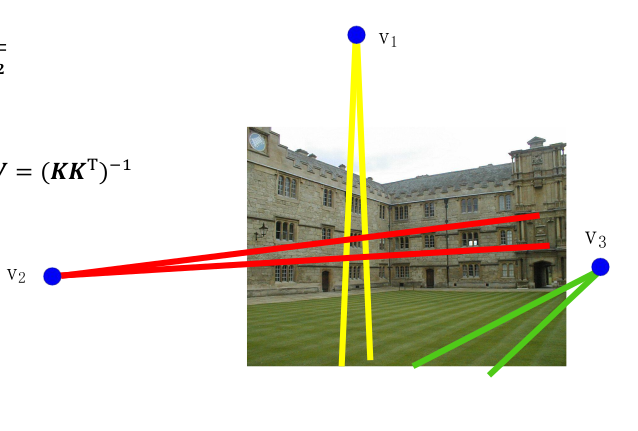
重构场景平面方向：

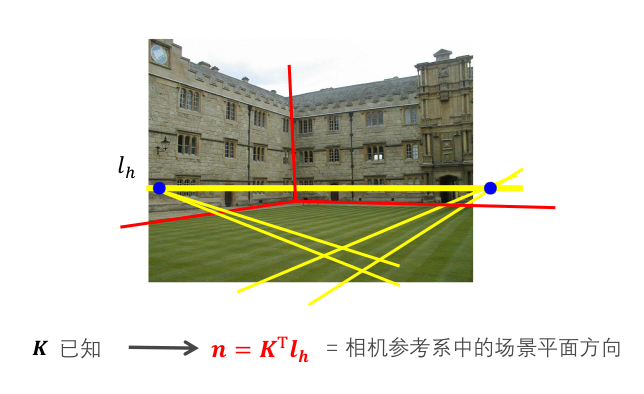
单视图重构缺陷： 场景的实际比例无法复制。

2、三维重建基础与极几何

2.1、三维重建基础

三角化求解问题： 已知： $p,p’,K,K’,R,T$ ，求解：$P$ 点的三维坐标？

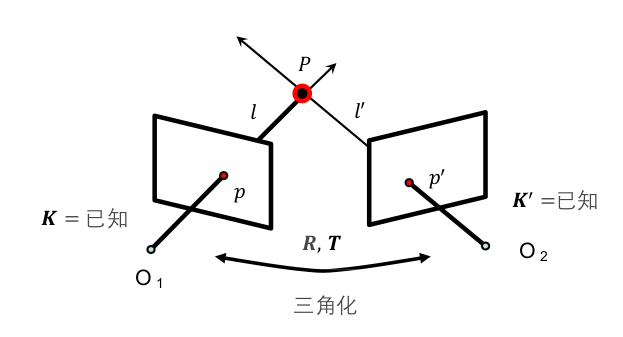
1. 线性求解：找到对应点对构建方程组求解。

$$\\ \begin{cases}\boldsymbol{p}=\boldsymbol{M}\boldsymbol{P}=\boldsymbol{K}(\boldsymbol{I}0)\boldsymbol{P}\\\\\boldsymbol{p}'=\boldsymbol{M}'\boldsymbol{P}=\boldsymbol{K}'(\boldsymbol{R}\boldsymbol{T})\boldsymbol{P}\end{cases} \\ \to \begin{cases}\begin{gathered} u={\frac{m_{1}P}{m_{3}P}} \rightarrow m_{1}P-u(\boldsymbol{m}_{3}P)=0 \\ v=\frac{m_{2}P}{m_{3}P} \rightarrow m_{2}P-v(\boldsymbol{m}_{3}\boldsymbol{P})=0 \\ u^{\prime}=\frac{m_{1}^{\prime}P}{m_{3}P} \rightarrow m_{1}^{\prime}P-u^{\prime}(\boldsymbol{m}_{3}^{\prime}\boldsymbol{P})=0 \\ v^{\prime}=\frac{m_{2}^{\prime}P}{m_{3}^{\prime}P} \to\boldsymbol{m}_2^{\prime}\boldsymbol{P}-v^{\prime}(\boldsymbol{m}_3^{\prime}\boldsymbol{P})=0 \end{gathered}\end{cases} \\ \to AP=0,A=\begin{pmatrix}u\boldsymbol{m}_3-\boldsymbol{m}_1\\v\boldsymbol{m}_3-\boldsymbol{m}_2\\u'\boldsymbol{m}_3'-\boldsymbol{m}_1'\\v'\boldsymbol{m}_3'-\boldsymbol{m}_2'\end{pmatrix}$$

方程数 4 个，未知参数 3 个，构成超定齐次线性方程组，采用最小二乘解：

  1. 对 $A$ 进行奇异值分解 $A=UDV^T$ ；
  2. $P$ 为 $V$ 矩阵的最后一列。

1. 非线性解法： 寻找 $P$ 最小化能量函数 $d(p,MP)+d(p’,M’P)$ ，采用牛顿法或L-M方法。

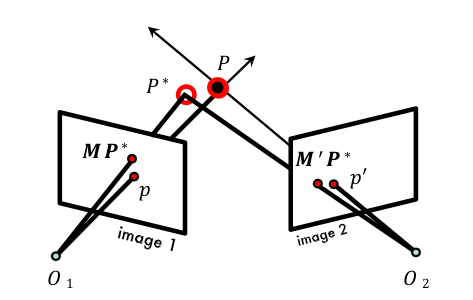
实际应用中存在的问题： 由于噪声存在，通常两条直线不相交，且线性、非线性方法都需要知道内参矩阵以及变换矩阵。

1. 问题1： 已知 $p,p’$ ，相机内参 $K,K’$ 。求解：相机间的 $R,T$ 以及 $P$ 的三维坐标？
2. 问题2： 已知 $p,p’$ 。求解：相机内参 $K,K’$ ，相机间的 $R,T$ 以及 $P$ 的三维坐标？

多视图几何的关键问题：

1. 相机几何：从一张或多张图像求解相机内、外参数；
2. 场景几何：通过两至多幅图寻找3D场景坐标；
3. 对应关系：已知一个图像中的 $p$ 点，如何在另一个图像中找到 $p’$ 点。

2.2、极几何与基础矩阵

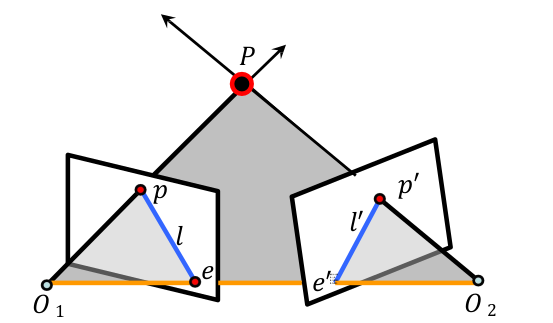
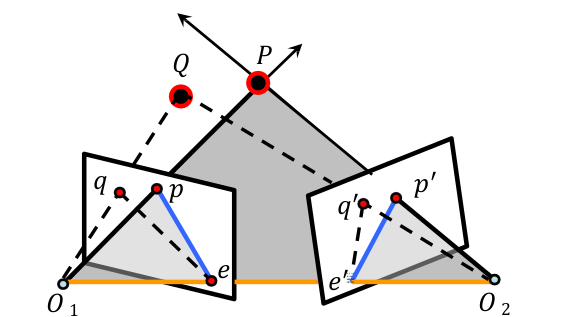
极几何： 描述了同一场景或者物体的两个视点图像间的几何关系。

• 概念：
  • 极平面：过点 $P,O_1,O_2$ 的平面；
  • 基线： $O_1,O_2$ 的连线；
  • 极线： 极平面与成像平面的交线；
  • 极点： 基线与成像平面的交点。
• 性质：
  • 极平面相交于基线；
  • 极线相交于极点；
  • $p(p’)$ 的对应点在极线 $l’(l)$ 上。
• 作用：将搜索范围缩小到对应的极线上。

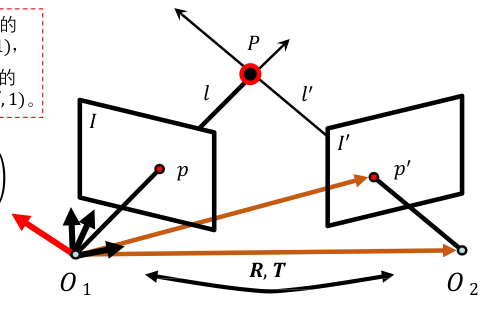
本质矩阵： 对 规范化相机 拍摄的两个视点图像间的极几何关系进行 代数描述。

• 推导：
  • $p’,O_2$ 在 $O_1$ 的坐标分别为：$R^{\mathrm{T}}p^{^{\prime}}-R^{\mathrm{T}}T$ ， $-R^TT$；
  • 上述两个向量的差乘垂直于极平面：$R^\mathrm{T}T\times(R^\mathrm{T}p^{\prime}-R^\mathrm{T}T)=R^\mathrm{T}T\times R^\mathrm{T}p^{\prime} = 0$ ；
  • 整理可得 $p^{\prime\text{T}} ( T \times R ) p = 0$ ；
  • 对上式进行整理：令 $E=T\times R=[T_\times]R$ ，$E$ 称为本质矩阵。即：$p’^TEp=0$ .

• 性质：
  • $p(p’)$ 对应的极线是 $l’(l’=Ep)(l(l=E^Tp’))$ ；
  • $Ee = 0$ 与 $e’^TE=0$ ；
  • $E$ 是奇异的（秩为2）；
  • $E$ 有 5个自由度 （三个旋转，三个平移，$det(E) = 0$ 去掉一个自由度）。

基础矩阵： 对 一般的透视相机 拍摄的两个视点图像间的极几何关系进行 代数描述 。

• 推导：参考本质矩阵推导。构建规范化相机模型。

  • $F={K^{\prime}}^{-\mathrm{T}}[T_{\times}]RK^{-1}$

• 性质：

  • $p(p’)$ 对应的极线是 $l’(l’=Fp)(l(l=F^Tp’))$ ；
  • $Fe = 0$ 与 $e’^TF=0$ ；
  • $F$ 是奇异的（秩为2）；
  • $F$ 有 7个自由度 （尺度无法确定，$det(E) = 0$ 去掉一个自由度）。

自由度问题： 参考：为什么本质矩阵５自由度，基础矩阵７自由度，单应矩阵８自由度？

2.3、基础矩阵估计

8点法： $F$ 共7个自由度，理论上7个点即可，但计算方法比较复杂。

$$(u^{\prime},v^{\prime},1)\begin{pmatrix}F_{11}&F_{12}&F_{13}\\F_{21}&F_{22}&F_{23}\\F_{31}&F_{32}&F_{33}\end{pmatrix}\begin{pmatrix}u\\v\\1\end{pmatrix}=0\quad\longrightarrow\quad(uu^{\prime},vu^{\prime},uv^{\prime},vv^{\prime},v^{\prime},u,v,1)\begin{pmatrix}F_{11}\\F_{12}\\F_{13}\\F_{21}\\F_{22}\\F_{23}\\F_{31}\\F_{33}\end{pmatrix}=0$$

求解：

1. 构建齐次系统 $Wf=0$ ；
2. 通常选取点对 $N>8$ ，构建最小二乘解，进行 SVD 分解求得 $\hat{F}$ 。$W$ 为点对矩阵，$f$ 为待求 $F$ 矩阵的向量形式， $f$ 为 $W$ 矩阵最小奇异值的右奇异向量，且 $|f|=1$

$$Wf=0\quad \to \quad \begin{aligned}&\min_f\|Wf\|\\&s.t.\parallel f\parallel=1\end{aligned} \quad \to \quad \hat{F}$$

$\hat{F}$ 并非我们所要求的基础矩阵：

• 原因：基础矩阵秩为 2， $\hat{F}$ 秩通常为3，即满秩。
• 解决：寻找 $F$ 最小化 $|F-\hat{F}|_F \quad s.t.det(F)=0$.

$${SVD(\widehat{F})=U\begin{pmatrix}s_1&{0}&{0}\\{0}&s_2&{0}\\{0}&{0}&{s_3}\end{pmatrix}V^\mathrm{T}}\quad\Longrightarrow\quad{F=U\begin{pmatrix}s_1&{0}&{0}\\{0}&s_2&{0}\\{0}&{0}&{0}\end{pmatrix}V^\mathrm{T}}$$

八点法： 步骤如下：

1. 构建 $W$ 矩阵；
2. 对 $W$ 矩阵进行奇异值分解求 $\hat{F}$ ；
3. 执行秩为 2 的约束求 $F$ ，即式（10）。

八点法缺陷： 精度较低， $W$ 矩阵中各个元素的数值差异过大。

归一化八点法： 解决八点法缺陷。**对每幅图施加变换 $T$ （平移和缩放），让其满足如下条件：

• 原点 = 图像上点的重心；
• 各个像点到坐标原点的均方根距离等于 $\sqrt{2}$ （或者均方距离等于2）。

1. 分别计算左图和右图的 $T$ 和 $T’$ ；
2. 坐标归一化 $q_i = Tp_i$ ，$q’_i = T’p’_i$ ；
3. 通过八点法计算矩阵 $F_q$ ；
4. 逆归一化 $F=T’_TF_qT$ 。