本文章是关于GAMES101课程的笔记。
一、曲线(Curves)
贝塞尔曲线: 重复对切线进行线性插值得到光滑曲线。
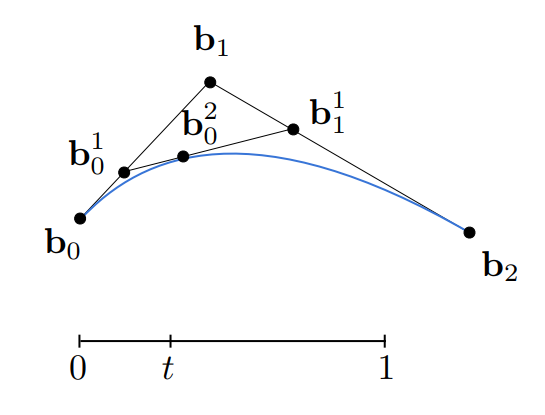
卡斯特里奥算法: 给定了系数的金字塔。
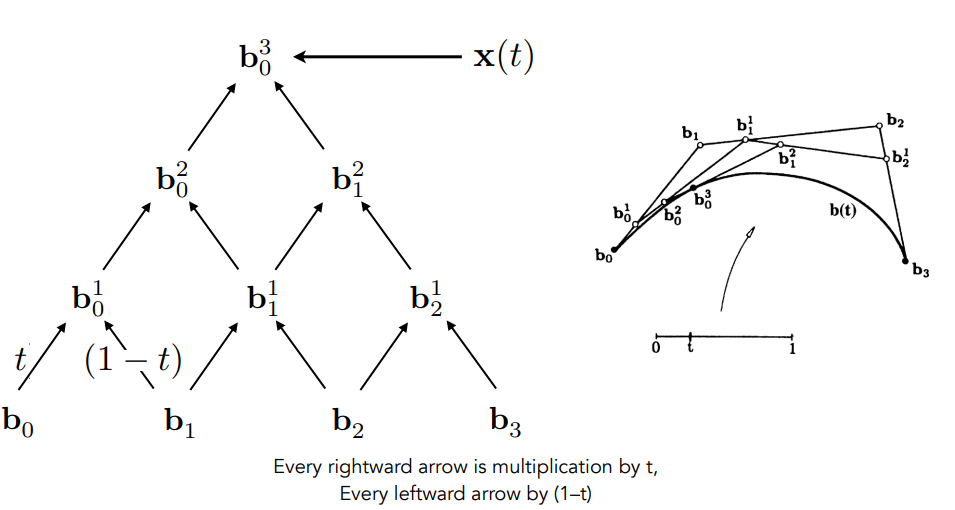
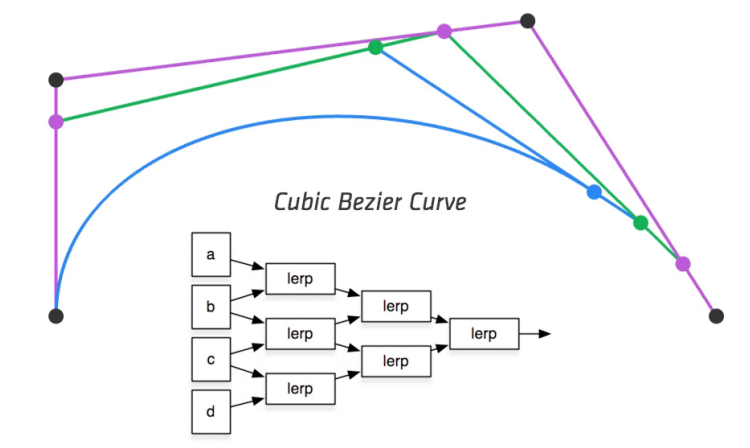
贝塞尔曲线本质: 多项式加权求和


贝塞尔曲线性质:
- 插值末端点;
- 与末端段相切;
- 仿射变化:控制点在进行仿射变换后绘制的贝塞尔曲线与之前的贝塞尔曲线相同;
- 凸包性质:曲线位于控制点的凸包内。
分段贝塞尔曲线的两种连续性:
$C^0$ 连续: 前一段末端端点和下一段第一端点相等
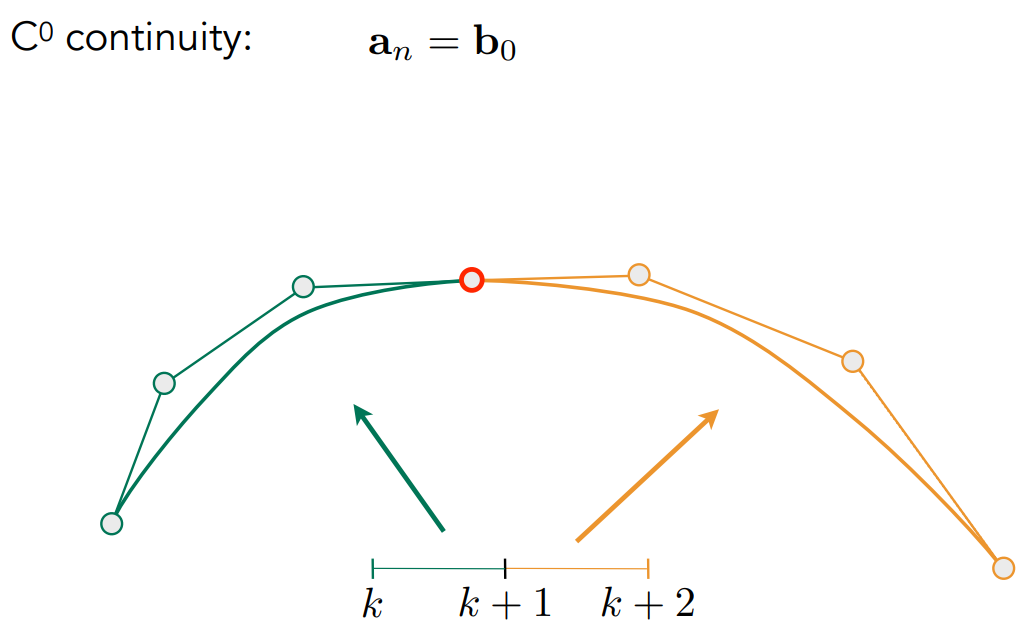
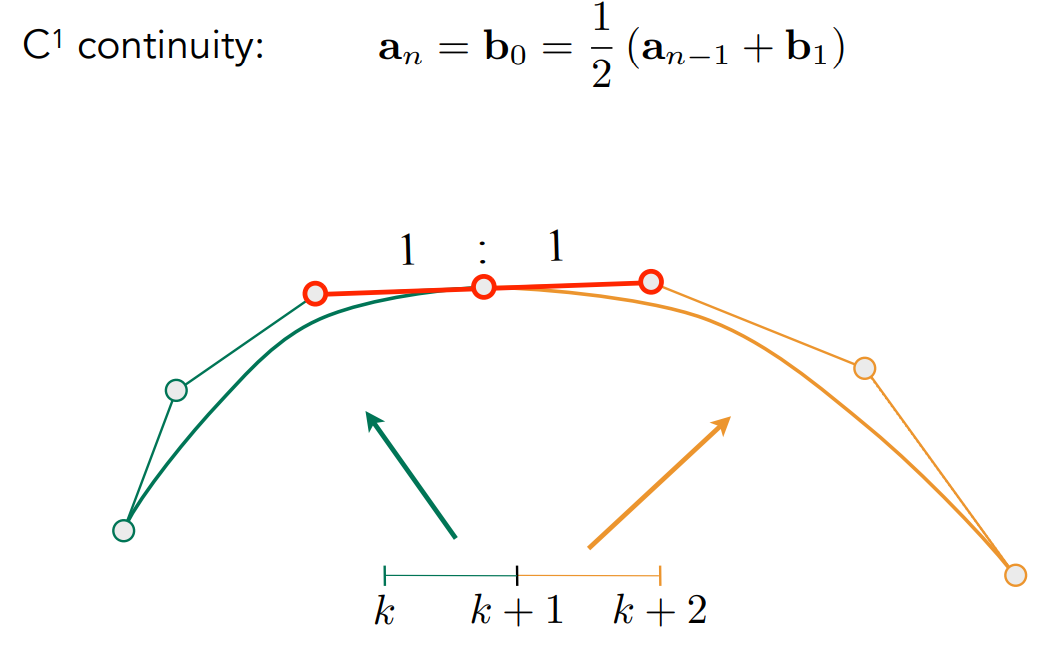
$C^1$ 连续:前一段末端端点和下一段第一端点相等,同时前一段倒数第二控制点和下一段第二控制点关于最后控制点对称。
样条: 构造为穿过给定点集并具有一定数量的连续导数的连续曲线。
B-样条: 构成样条的基本单元(类似基函数)。
二、曲面(Surfaces)
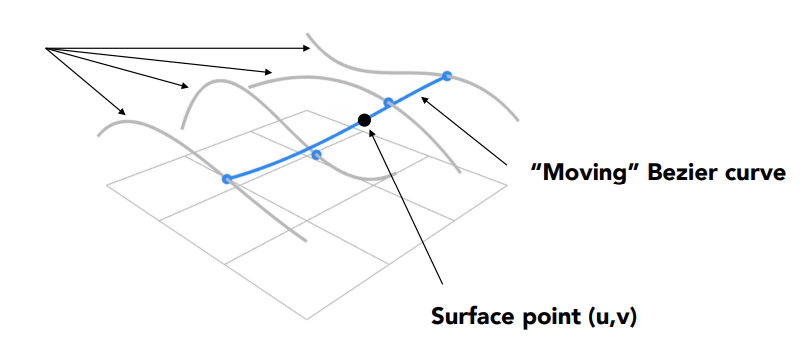
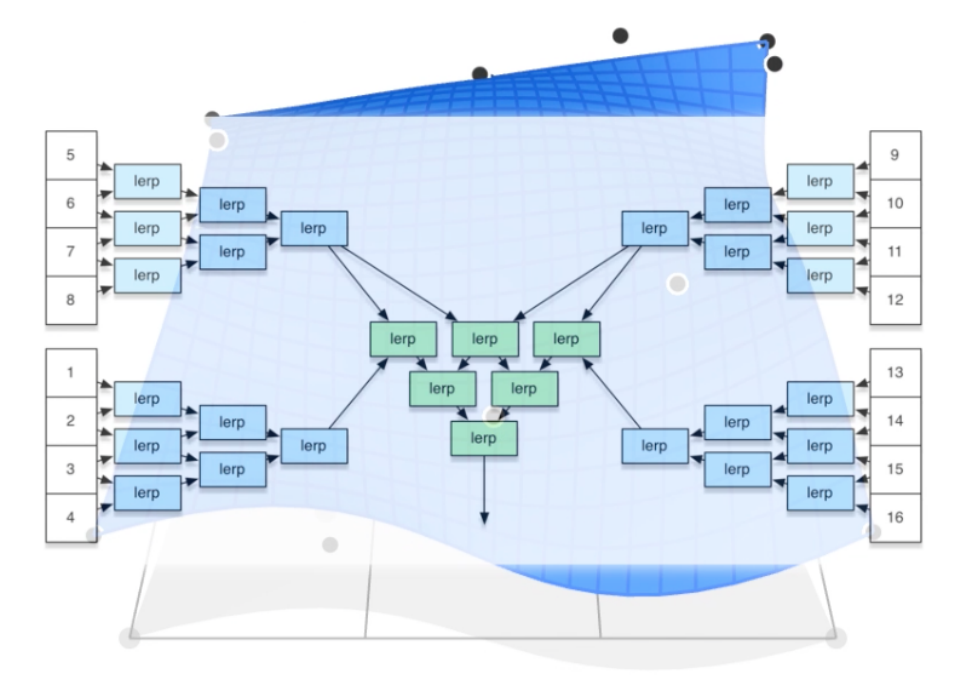
贝塞尔曲面: 对一个二维平面进行两次贝塞尔变化。(以 $4\times4$ 为例)
- 使用 de Casteljau 计算 $u$中 4 条贝塞尔曲线中每一条上的点 $u$。 这为“移动”贝塞尔曲线提供了 4 个控制点;
- 使用一维 de Casteljau 评估“移动”曲线上的 v 点。
三、细分(Subdivison)
Loop Subdivision: 分割三角形的一种方法,对每条边的新的顶点进行 加权平均 , 形成新的三角形。
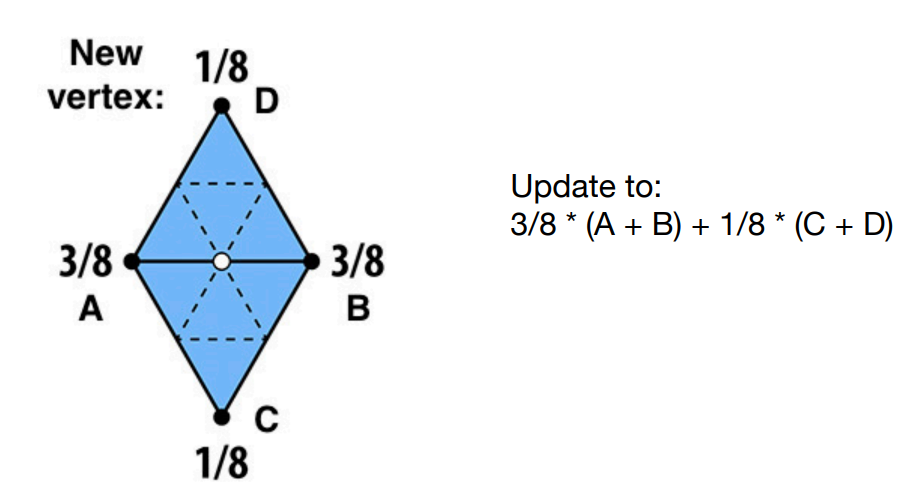
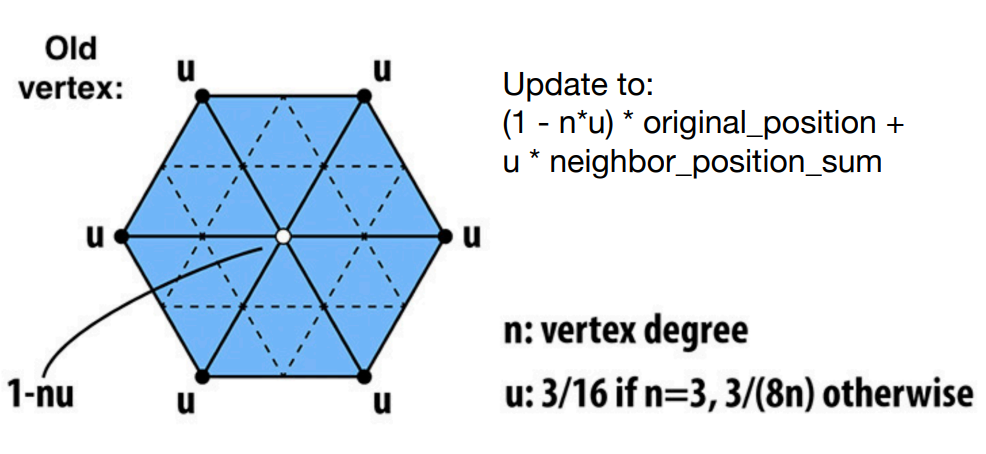
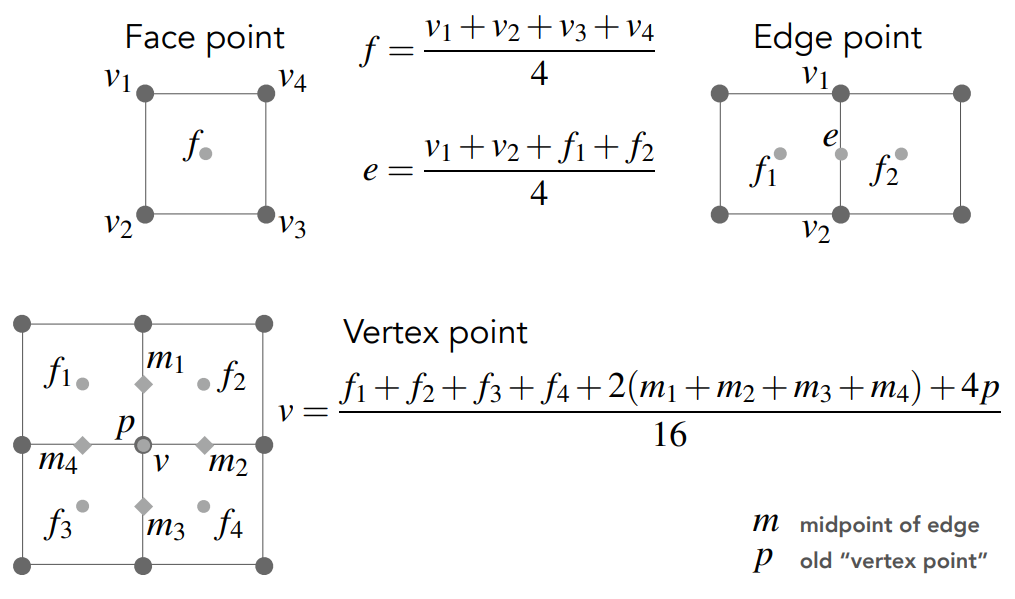
Catmull-Clark Subdivision:
- 在每个平面添加新的端点;
- 在每条边添加中点;
- 连接所有新的端点。
奇异点(Extraordinary vertex): 度不为 4 的点
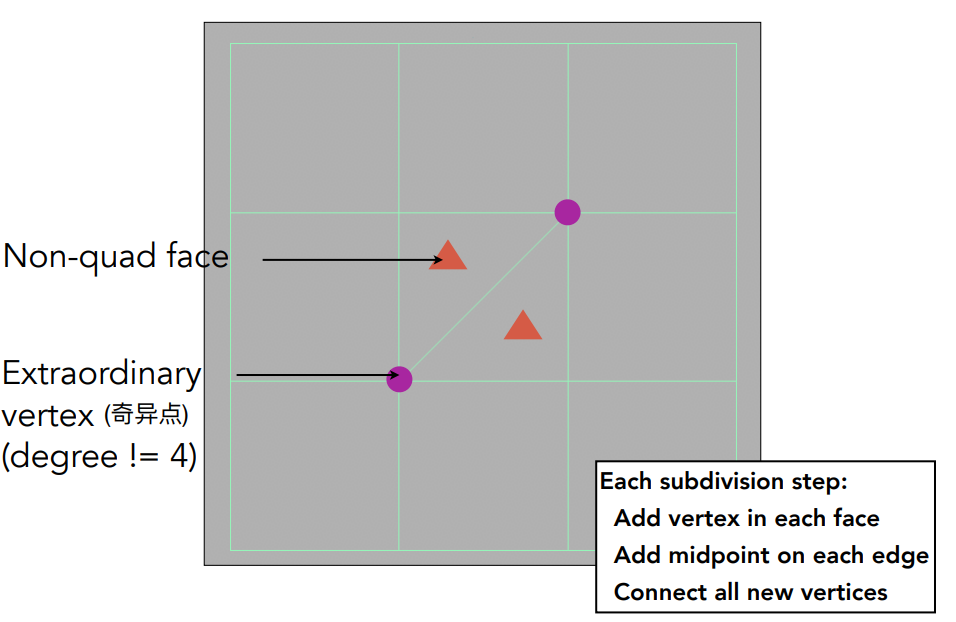
- 每个非四边形面会产生新的奇异点;
- 奇异点对应的度小于 4;
- 增加了新的四边形面。
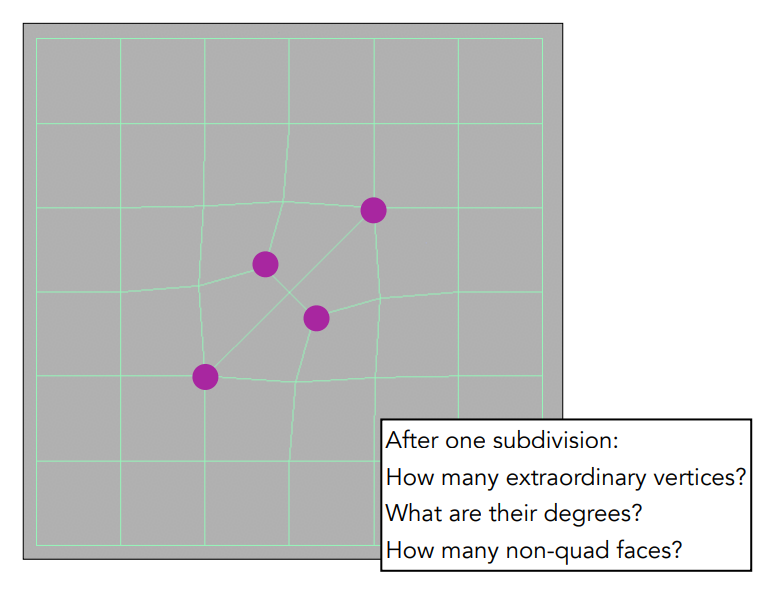
更新公式:
四、简化(Simplification)
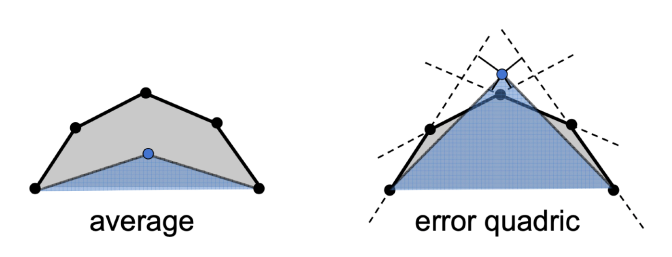
边缘塌陷(Edge Collapsing): 将多条边进行合并
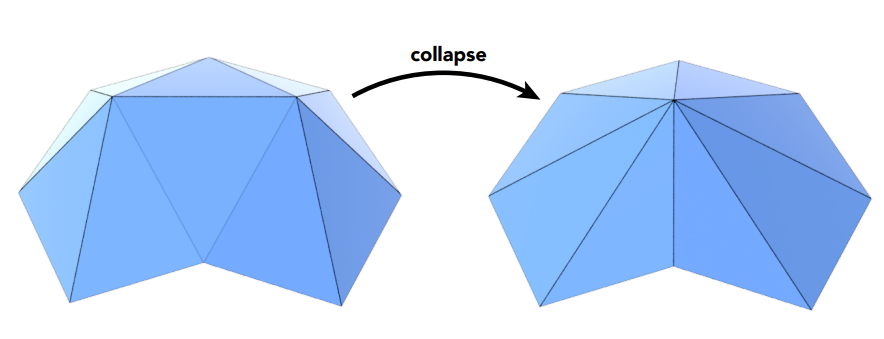
二次误差度量(Quadric Error Metrics): 如何进行边缘塌陷的一种优化方法——最小化二次误差。