AppZ99's Blog

OHHHH

0%

代码随想录-随记——数据结构篇

发表于 更新于
本文字数： 7.1k 阅读时长 ≈ 6 分钟

本文主要是对《代码随想录》中数据结构部分的知识点做简要的笔记。

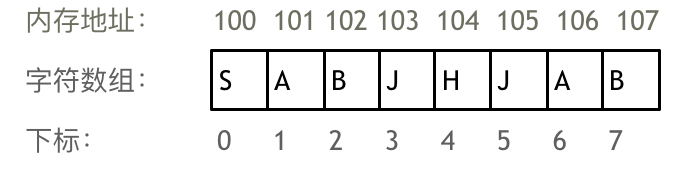
1、数组

1.1、数组理论基础

概念： 数组是存放在连续内存空间上的相同类型数据的集合。

image-20230905231004040

注意：

  • 数组下标从 0 开始；
  • 数组内存空间的地址是连续的。

数组操作的复杂性： 正是由于数组内存地址是连续的，所以在对数组进行删除和添加的操作时，难免需要移动其他元素的地址。

不可删除性： 数组的元素是不能删除的，只能覆盖。

C++ 中的 vector 和 array: vector 底层实现是 array，本质不是数组而是容器。

C++ 二维数组的地址空间： C++ 二维数组在地址空间上是连续的。

1.2、二分查找

二分查找的主要问题在于边界的确定。一半采用两种写法：

  • 左闭右闭
  • 左闭右开
  1. 左闭右闭
1
2
3
4
5
6
7
8
9
10
11
12
13
14
int left = 0;
int right = nums.size() - 1;	// 闭区间故需要取值
while(left <= right){  	// 区间合理
    int middle = left + (right - left) / 2;
    if(nums[middle] > target){
        right = middle - 1;	// 已经大于，故不用在取 middle
    }
    else if(nums[middle] < target){
        left = middle + 1;	// 上述同理
    }
    else{
        return middle;
    }
}
  1. 左闭右开
1
2
3
4
5
6
7
8
9
10
11
12
int left = 0;
int right = nums.size(); // 即：[left, right)
while (left < right) { // 因为left == right的时候，在[left, right)是无效的空间，所以使用 <
    int middle = left + ((right - left) >> 1);
    if (nums[middle] > target) {
        right = middle; // target 在左区间，在[left, middle)中
    } else if (nums[middle] < target) {
        left = middle + 1; // target 在右区间，在[middle + 1, right)中
    } else { // nums[middle] == target
        return middle; // 数组中找到目标值，直接返回下标
    }
}

运用二分查找的关键词：有序数组、元素唯一 。

1.3、删除元素

题意：删除数组中指定的某个值的元素。

  1. 暴力解法：for循环遍历
  2. 双指针解法：重点在于理解双指针中快慢指针的意义：
    1. 快指针：寻找新数组的元素，新数组就是不含有目标元素的数组；
    2. 慢指针：指向更新新数组的下标位置。

1.4、有序数组的平方

LeetCode997.有序数组的平方

将双指针思想应用在相向的思想。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    vector<int> sortedSquares(vector<int>& A) {
        int k = A.size() - 1;
        vector<int> result(A.size(), 0);
        for (int i = 0, j = A.size() - 1; i <= j;) { // 注意这里要i <= j，因为最后要处理两个元素
            if (A[i] * A[i] < A[j] * A[j])  {
                result[k--] = A[j] * A[j];
                j--;
            }
            else {
                result[k--] = A[i] * A[i];
                i++;
            }
        }
        return result;
    }
};

1.5、长度最小的子数组

LeetCode209.长度最小的子数组

本题最主要的是滑动窗口的思想。

滑动窗口： 不断调节子序列的起始位置和终止位置，从而得出我们想要的结果；

for循环中的移动变量： 移动变量应该是终止位置，如果是起始位置开始遍历，跟双for循环无异。

滑动窗口需要确定如下三点：

  • 窗口内是什么？
  • 如何移动窗口的起始位置？
  • 如何移动窗口的结束位置？

精髓： 不断调节子序列的起始位置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int minSubArrayLen(int s, vector<int>& nums) {
        int result = INT32_MAX;
        int sum = 0; // 滑动窗口数值之和
        int i = 0; // 滑动窗口起始位置
        int subLength = 0; // 滑动窗口的长度
        for (int j = 0; j < nums.size(); j++) {
            sum += nums[j];
            // 精髓所在：如何决定起始位置
            // 注意这里使用while，每次更新 i（起始位置），并不断比较子序列是否符合条件
            while (sum >= s) {
                subLength = (j - i + 1); // 取子序列的长度
                result = result < subLength ? result : subLength;
                sum -= nums[i++]; // 这里体现出滑动窗口的精髓之处，不断变更i（子序列的起始位置）
            }
        }
        // 如果result没有被赋值的话，就返回0，说明没有符合条件的子序列
        return result == INT32_MAX ? 0 : result;
    }
};

最小滑窗模板和最大滑窗模板

参考：

LeetCode904.水果成蓝

【深度解析】这道题和76. 最小覆盖子串的区别

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// 904
class Solution {
public:
    int totalFruit(vector<int>& fruits) {
        int n = fruits.size();
        unordered_map<int, int> cnt;

        int left = 0, ans = 0;
        for(int right = 0; right < n; right++){
            ++cnt[fruits[right]];
            while(cnt.size() > 2){
                auto it = cnt.find(fruits[left]);
                --it->second;
                if(it->second == 0){
                    cnt.erase(it);
                }
                ++left;
            }
            ans = max(ans, right - left + 1);
        }
        return ans;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// 最小滑窗模板
while j < len(nums):
    判断[i, j]是否满足条件
    while 满足条件：
        不断更新结果(注意在while内更新！)
        i += 1 （最大程度的压缩i，使得滑窗尽可能的小）
    j += 1

// 最大滑窗模板
while j < len(nums):
    判断[i, j]是否满足条件
    while 不满足条件：
        i += 1 （最保守的压缩i，一旦满足条件了就退出压缩i的过程，使得滑窗尽可能的大）
    不断更新结果（注意在while外更新！）
    j += 1

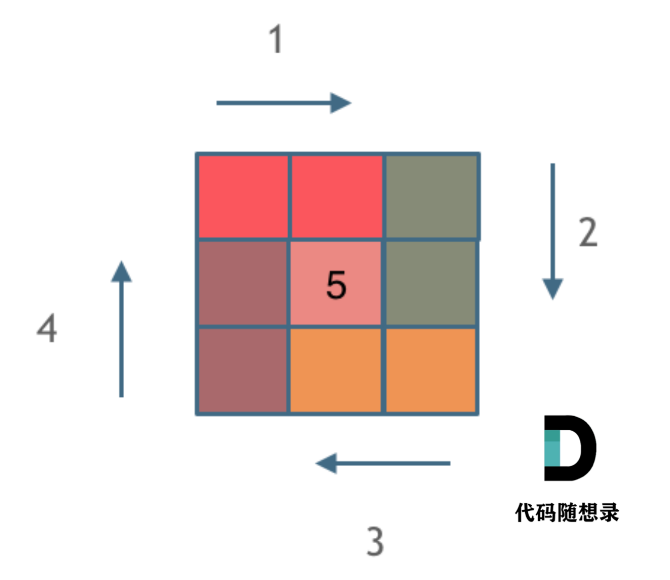
1.6、螺旋矩阵II

LeetCode59.螺旋矩阵II

核心所在： 与二分法一样要坚持 循环不变量原则 ，具体而言就是边界信息不变，是左闭右开还是左闭右闭。确认好后依次循环。

image-20230920225702829

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        vector<vector<int>> res(n, vector<int>(n, 0)); // 使用vector定义一个二维数组
        int startx = 0, starty = 0; // 定义每循环一个圈的起始位置
        int loop = n / 2; // 每个圈循环几次，例如n为奇数3，那么loop = 1 只是循环一圈，矩阵中间的值需要单独处理
        int mid = n / 2; // 矩阵中间的位置，例如：n为3， 中间的位置就是(1，1)，n为5，中间位置为(2, 2)
        int count = 1; // 用来给矩阵中每一个空格赋值
        int offset = 1; // 需要控制每一条边遍历的长度，每次循环右边界收缩一位
        int i,j;
        while (loop --) {
            i = startx;
            j = starty;

            // 下面开始的四个for就是模拟转了一圈
            // 模拟填充上行从左到右(左闭右开)
            for (j = starty; j < n - offset; j++) {
                res[startx][j] = count++;
            }
            // 模拟填充右列从上到下(左闭右开)
            for (i = startx; i < n - offset; i++) {
                res[i][j] = count++;
            }
            // 模拟填充下行从右到左(左闭右开)
            for (; j > starty; j--) {
                res[i][j] = count++;
            }
            // 模拟填充左列从下到上(左闭右开)
            for (; i > startx; i--) {
                res[i][j] = count++;
            }

            // 第二圈开始的时候，起始位置要各自加1， 例如：第一圈起始位置是(0, 0)，第二圈起始位置是(1, 1)
            startx++;
            starty++;

            // offset 控制每一圈里每一条边遍历的长度
            offset += 1;
        }

        // 如果n为奇数的话，需要单独给矩阵最中间的位置赋值
        if (n % 2) {
            res[mid][mid] = count;
        }
        return res;
    }
};

2、链表

2.1、链表理论基础

概念： 链表是一种通过指针串联在一起的线性结构，每一个节点由两部分组成，一个是数据域一个是指针域（存放指向下一个节点的指针），最后一个节点的指针域指向null（空指针的意思）。

链表的类型：

  • 单链表
  • 双链表
  • 循环链表

链表的存储方式： 链表是通过指针域的指针链接在内存中各个节点。所以链表中的节点在内存中不是连续分布的，而是散乱分布在内存中的某地址上，分配机制取决于操作系统的内存管理。

2.2、删除链表元素

LeetCode203.移除链表元素

操作链表主要涉及两种操作：

  • 直接使用原来的链表来进行删除操作。
  • 设置一个虚拟头结点在进行删除操作。

在直接使用原链表的操作中，需要对头节点和一般节点做区别操作，故采用虚拟头节点可以使用统一的方式去对链表进行操作。

2.3、设计链表

LeetCode707.设计链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
class MyLinkedList {
public:
    // 定义链表节点结构体
    struct LinkedNode {
        int val;
        LinkedNode* next;
        LinkedNode(int val):val(val), next(nullptr){}
    };

    // 初始化链表
    MyLinkedList() {
        _dummyHead = new LinkedNode(0); // 这里定义的头结点 是一个虚拟头结点，而不是真正的链表头结点
        _size = 0;
    }

    // 获取到第index个节点数值，如果index是非法数值直接返回-1， 注意index是从0开始的，第0个节点就是头结点
    int get(int index) {
        if (index > (_size - 1) || index < 0) {
            return -1;
        }
        LinkedNode* cur = _dummyHead->next;
        while(index--){ // 如果--index 就会陷入死循环
            cur = cur->next;
        }
        return cur->val;
    }

    // 在链表最前面插入一个节点，插入完成后，新插入的节点为链表的新的头结点
    void addAtHead(int val) {
        LinkedNode* newNode = new LinkedNode(val);
        newNode->next = _dummyHead->next;
        _dummyHead->next = newNode;
        _size++;
    }

    // 在链表最后面添加一个节点
    void addAtTail(int val) {
        LinkedNode* newNode = new LinkedNode(val);
        LinkedNode* cur = _dummyHead;
        while(cur->next != nullptr){
            cur = cur->next;
        }
        cur->next = newNode;
        _size++;
    }

    // 在第index个节点之前插入一个新节点，例如index为0，那么新插入的节点为链表的新头节点。
    // 如果index 等于链表的长度，则说明是新插入的节点为链表的尾结点
    // 如果index大于链表的长度，则返回空
    // 如果index小于0，则在头部插入节点
    void addAtIndex(int index, int val) {

        if(index > _size) return;
        if(index < 0) index = 0;        
        LinkedNode* newNode = new LinkedNode(val);
        LinkedNode* cur = _dummyHead;
        while(index--) {
            cur = cur->next;
        }
        newNode->next = cur->next;
        cur->next = newNode;
        _size++;
    }

    // 删除第index个节点，如果index 大于等于链表的长度，直接return，注意index是从0开始的
    void deleteAtIndex(int index) {
        if (index >= _size || index < 0) {
            return;
        }
        LinkedNode* cur = _dummyHead;
        while(index--) {
            cur = cur ->next;
        }
        LinkedNode* tmp = cur->next;
        cur->next = cur->next->next;
        delete tmp;
        //delete命令指示释放了tmp指针原本所指的那部分内存，
        //被delete后的指针tmp的值（地址）并非就是NULL，而是随机值。也就是被delete后，
        //如果不再加上一句tmp=nullptr,tmp会成为乱指的野指针
        //如果之后的程序不小心使用了tmp，会指向难以预想的内存空间
        tmp=nullptr;
        _size--;
    }

    // 打印链表
    void printLinkedList() {
        LinkedNode* cur = _dummyHead;
        while (cur->next != nullptr) {
            cout << cur->next->val << " ";
            cur = cur->next;
        }
        cout << endl;
    }
private:
    int _size;
    LinkedNode* _dummyHead;

};

2.4、翻转链表

LeetCode206.翻转链表

主要采用双指针的思想进行求解，其中重点在于：

  • 何时结束：指到 nullptr 时；
  • 交换的顺序

采用递归的写法其思想也是双指针思想，重点在于传入参数：把xx值赋给xx，决定了递归的传参

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    ListNode* reverse(ListNode* pre,ListNode* cur){
        if(cur == NULL) return pre;
        ListNode* temp = cur->next;
        cur->next = pre;
        // 可以和双指针法的代码进行对比，如下递归的写法，其实就是做了这两步
        // pre = cur;
        // cur = temp;
        return reverse(cur,temp);
    }
    ListNode* reverseList(ListNode* head) {
        // 和双指针法初始化是一样的逻辑
        // ListNode* cur = head;
        // ListNode* pre = NULL;
        return reverse(NULL, head);
    }

};