【笔记】基于图像的三维重建——纹理图像生成

本文主要关于深蓝学院系列课程——基于图像的三维重建的笔记。

课程链接 基于图像的三维重建

1、纹理图像的自动创建

1.1、基础知识

纹理贴图： 同一三维模型采用不同纹理图案进行渲染。

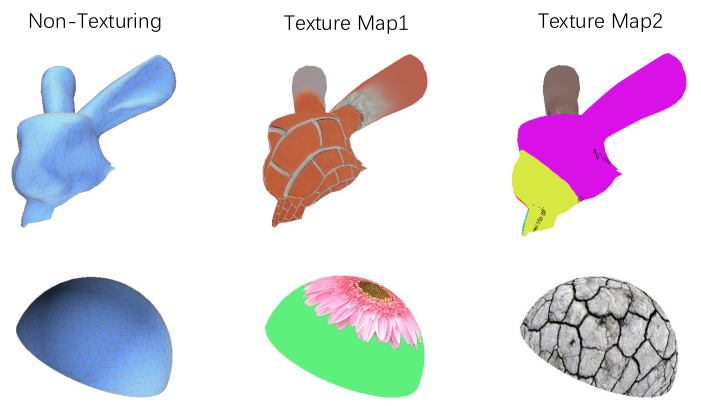
纹理坐标： 三维网格中的面片与纹理图像的映射关系。

基本算法流程：

1. 输入模型
2. 模型参数化
3. 纹理图像绘制
4. 纹理模型

纹理图像的创建方式：

• 交互软件
• 自动计算

1.2、纹理图像的自动创建

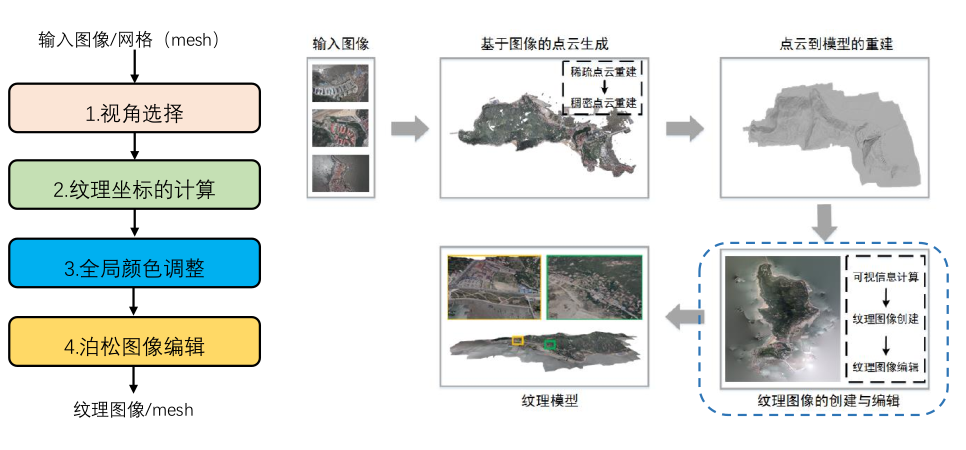
算法流程：

1. 视角选择
2. 纹理坐标的计算
3. 全局颜色调整
4. 柏松图像编辑

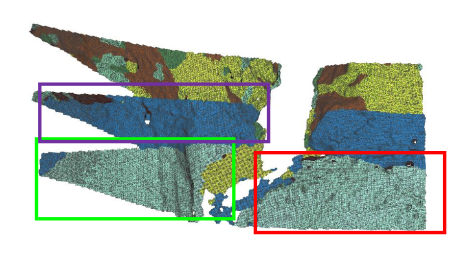
视角选择：

选择标准：

• 图像的尺寸
• 图像的细节丰富程度
• 图像的可视化
• 邻域平滑性

数学模型：

• 将视角选择建模成多标签的分配问题：为每一个三角形分配一个标签（视角）；
• 将网格上建立 MRF 随机场，每个面片代表随机场的一个顶点；
• 能量函数分为数据项 $E_{data}$ 和平滑项 $E_{smooth}$

$$E(l)=\sum_{F_i\in\mathrm{Faces}}E_{\mathrm{data}}(F_i,l_i)+\sum_{(F_i,F_j)\in\mathrm{Edges}}E_{\mathrm{smooth}}(F_i,F_j,l_i,l_j)$$

数据项：

• 图像质量：
  • 纹理细节：投影三角形的平均梯度；
  • 尺度：投影三角形的面积。

$$E_\text{data}=-\int_{\phi(F_i,l_i)}\|\nabla(I_{l_i}(p))\|_2\mathrm{d}p \\ \begin{aligned} &l_{i}\quad \text{表示视角}; \\ &\nabla\left(I_{l_{i}}(p)\right)\quad \text{表示投影点处的梯度;} \\ &\phi(F_{i},l_{i})\quad \text{表示三角形的投影区域。} \end{aligned}$$

• 可视性：

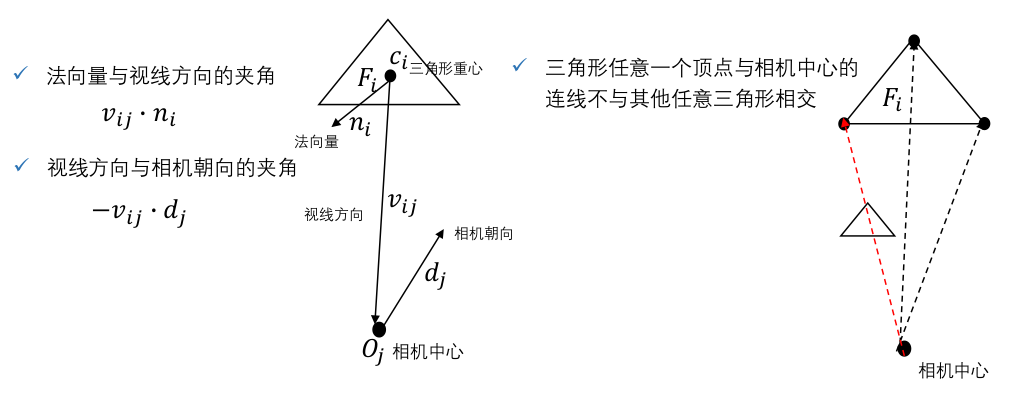
平滑项：通过保持邻域的平滑性使得相邻三角形有相同的视角，从而可以减少缝隙为后续的处理提供便利。

$$E_{\mathrm{smooth}}=[l_i\neq l_j]\\ [\quad] \text{为艾佛森括号（Iverson bracket）}$$

MRF 视角选择常用优化方法：

• $\alpha - expansion$
• $\alpha-\beta \quad swap$

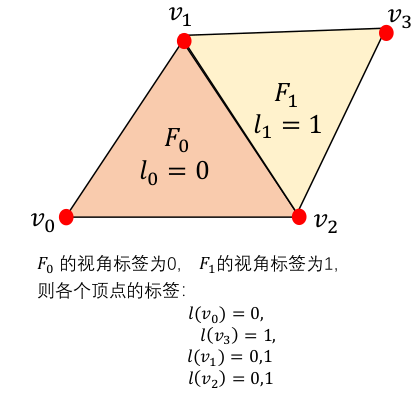
顶点处的视角标签：

视角选择是以 facet 为优化对象，边界上的 Vertex 会具有所有相邻 facet 的标签，即具有多个纹理坐标。

纹理坐标的计算：

• 投影到对应的图像上，街区最小包围盒范围内的图像作为纹理图像；

• 投影的坐标归一化后作为纹理坐标；

全局颜色调整：

问题引入：由于不同视角间存在相机曝光或者光照差异导致不同， Texture Patch 边界处存在明显缝隙。

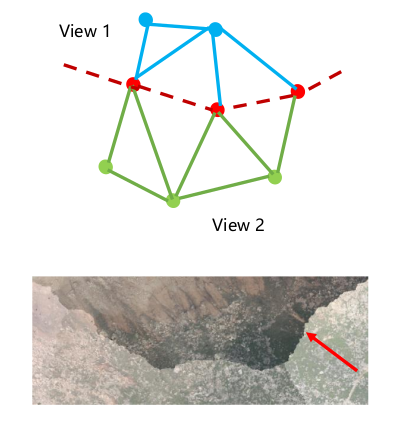
解决思路：每个像素添加一个颜色调整量使得：

• 缝隙处的颜色差异尽量小；
• Patch 内部相邻像素的调整尽量近似。

参数量爆炸问题：

• 每个像素对应一个参数，使得整体参数量过大，计算量太大？
• 解决：仅考虑顶点处的色彩调整量
  • 首先为每个顶点 $v_i$ ，添加一个调整量 $g_i$ ；
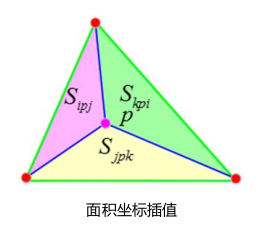
  • 通过插值的方式得到每个像素的调整值

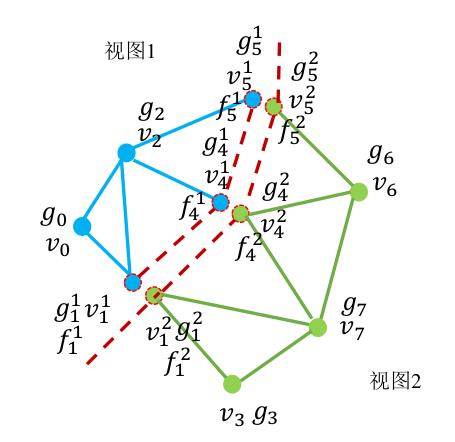
缝隙处顶点的调整量定义问题：

对缝隙处的顶点进行拆分，假设缝隙上的顶点 $v_i$ 的视角标签为 $\boldsymbol{l}_{i}=\{l_{i}^{0},l_{i}^{1},…l_{i}^{n_{v_{i}}-1}\},n_{v_{i}}$ 为标签个数，则顶点 $v_i$ 将被分为 $n_{v_i}$ 个顶点。

$$v_{i}\rightarrow\{v_{i}^{l_{i}^{0}},v_{i}^{l_{i}^{1}},...,v_{i}^{l_{i}^{n_{v_{i}-1}}}\}$$

相应的颜色调整量 $g_i$ ：

$$g_{i}\rightarrow\{g_{i}^{l_{i}^{0}},g_{i}^{l_{i}^{1}},\ldots,g_{i}^{l_{i}^{n_{v_{i}-1}}}\}$$

变量总个数：

$$\sum_i^Nn_{v_i}$$

函数能量定义为：$f_{i}^{l_{i}^{j}}$ 表示 $v_i$ 在视角 $l_{i}^j$ 中的颜色

$$\begin{gathered} E(g) =\sum_{v_{i}\in seam}\sum_{(l_{i}^{j},l_{i}^{k})\in l_{i}}\left(f_{i}^{l_{i}^{j}}+g_{i}^{l_{i}^{j}}-(f_{i}^{l_{i}^{k}}+g_{i}^{l_{i}^{k}})\right)^{2} +\lambda\sum_{v_{i}}\sum_{v_{j}\in N(v_{i})}\sum_{l\in l_{i}\cap l_{j}}(g_{i}^{l}-g_{j}^{l})^{2} \end{gathered}$$

建模后的能量函数一般为 稀疏线性方程 ，针对大规模的线性稀疏方程可以采用 **共轭梯度法（Conjugate Gradient）进行优化。

柏松图像编辑：

问题引入：对于缝隙比较严重的区域，全局颜色调整并不能保证完全去除缝隙，还需要进一步处理。

算法原理：

• 边界上的像素值与背景图像相同；
• 前景区域内的梯度与引导梯度场相同。

数学模型：

$$min_f\iint_{\Omega}|\nabla f-\boldsymbol{v}|,wrt.f|_{\partial\Omega}=f^*|_{\partial\Omega} \\ \text{等价于：}\Delta f=\operatorname{div}\boldsymbol{v}over\Omega,wrt.f|_{\partial\Omega}=f^*|_{\partial\Omega}\\\\ \begin{aligned} &\text{v 是引导梯度场}&& \text{S 是背景区域} \\ &\text{Ω 是前景区域}&& f^* 是背景区的光度函数 \\ &\partial\Omega 是边界区域&& \text{f 是待求的前景区的光度函数} \end{aligned} \\ \operatorname{\text{其中}div}\boldsymbol{v}={\frac{\partial u}{\partial x}}+{\frac{\partial v}{\partial y}},{\text{是梯度}}\boldsymbol{v}=(u,v)\text{的散度}$$

散度计算：

$$\begin{array}{c}\Delta f(p,q)=f_{p-1,q}+f_{p,q-1}+f_{p,q+1}+f_{p+1,q}-4*f_{p,q}\end{array}$$

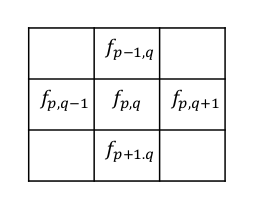
能量函数通过构建线性系统进行求解：

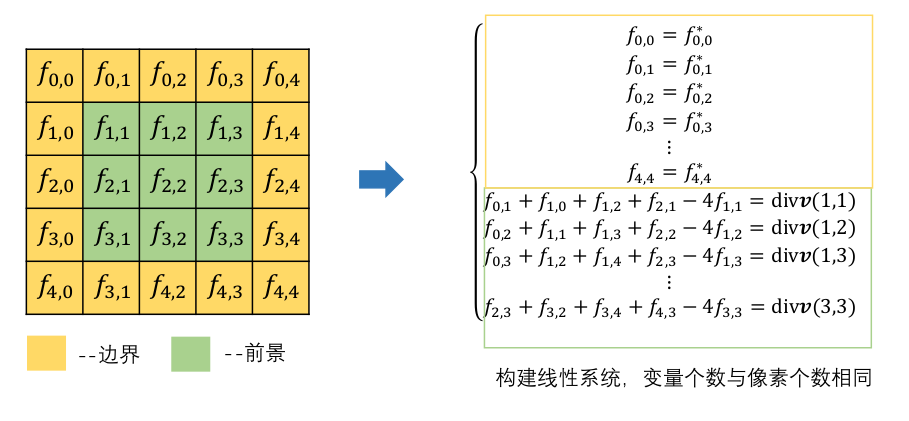
加速策略：

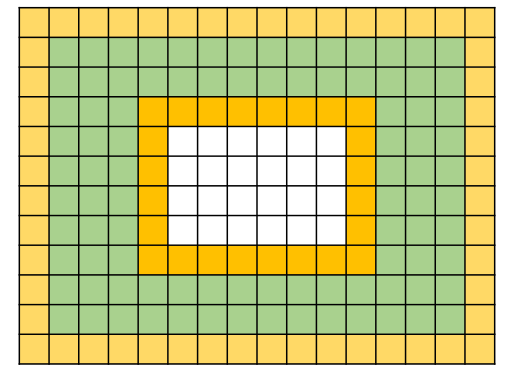
• 进行全局颜色调整之后，只需要在缝隙处进行泊松编辑即可；
• 可以通过控制内部区域的范围，（如由当前边界往前景区域扩充3个像素的作为前景进行计算），从而减少线性系统的规模。

OBJ 文件：

2、基于光度一致性的网格细节优化

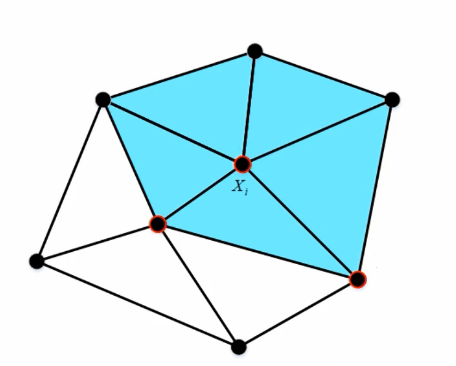
离散网格上定义能量函数：

每个顶点的梯度相当于 $1-ring$ 范围内所有点的梯度的加权和。

$$\frac{\mathrm{d}\mathrm{E}(S)}{\mathrm{d}X_i}=\int_S\phi_i(x)\nabla\mathrm{E}(x)\mathrm{d}x\quad i\in[1,n]$$

基于 surface 的光度一致性的度量：

$$\mathrm{E}_{\mathrm{error}}(S)=\sum_{i,j}\int_{\Omega_{ij}^S}h(I_i,I_{ij}^S)(x_i)\mathrm{d}x_i,$$

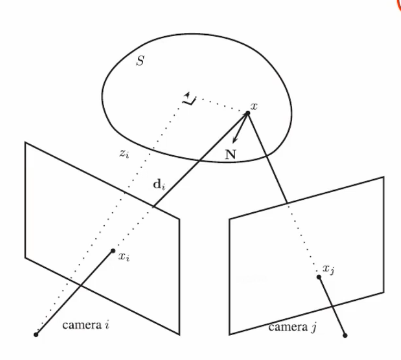
• $h(I,J)(x_{i})$ 表示在图像 $I$ 和 $J$ 之间在像素 $x_i$ 处的光度一致性；
• $I_{ij}^{S}=I_{j}\circ\prod_{j}\circ\prod_{i}^{-1}$ 表示将图像 $I_j$ 通过曲面 $S$ 重投影到图像 $I_i$ 上；
• $\Omega_{ij}^{\mathcal{S}}$ 表示重投影的有效区域；
• $\prod_i$ 和 $\prod_i^{-1}$ 分别表示第 $i$ 帧图像的投影和逆投影。

$$\begin{aligned} &\mathrm{E}_{\mathrm{error}}(S)=\sum_{i,j}\int_{\Omega_{ij}^{S}}h(I_{i},I_{ij}^{S})(x_{i})\mathrm{d}x_{i} \\ &\operatorname{E}_{\mathrm{error}}(S)=\sum_{i,j}\mathcal{M}_{ij}(S) \\ &\nabla\mathrm{E}_{\mathrm{error}}(S)=\sum_{i,j}\nabla\mathcal{M}_{ij}(S). \end{aligned}$$

• 其中 $\mathrm{d}x_i=-\mathbf{N}^T\mathbf{d}_i\mathrm{d}x/z_i^3$

$$\begin{aligned} &\nabla\mathcal{M}_{ij}(x)=-\left[\partial_{2}M(x_{i})DI_{j}(x_{j})D\Pi_{j}(x)\frac{\mathbf{d}_{i}}{z_{i}^{3}}\right]\mathbf{N} \\\\ &\begin{aligned}f_{ij}(x_{i})=\partial_{2}M(x_{i})DI_{j}(x_{j})D\Pi_{j}(x)\mathbf{d}_{i}\end{aligned} \\\\ &\nabla\mathcal{M}_{ij}(x)=-f_{ij}(x_{i})\mathbf{N}/z_{i}^{3} \end{aligned}$$

得到：

$$\begin{aligned} &{\frac{\mathrm{d}\mathrm{E}_{\mathrm{error}}(S)}{\mathrm{d}X}}=\int_{S}\phi(x)\sum_{i,j}\nabla\mathcal{M}_{ij}(x)\mathrm{d}x \\ &=-\int_{S}\phi(x)\sum_{i,j}f_{ij}(x_{i})\mathbf{N}/z_{i}^{3}\mathrm{d}x \\ &=-\sum_{ii}\int_{S}\phi(x)f_{ij}(x_{i})\mathbf{N}/z_{i}^{3}\mathrm{d}x \end{aligned}$$

根据$\mathrm{d}x_i=-\mathbf{N}^T\mathbf{d}_i\mathrm{d}x/z_i^3$ ：

$$\begin{aligned} &{\frac{\mathrm{d}\mathrm{E}_{\mathrm{error}}(S)}{\mathrm{d}X}}=\int_{S}\phi(x)\sum_{i,j}\nabla\mathcal{M}_{ij}(x)\mathrm{d}x \\ &=\sum_{i,j}\int_{\Omega_{ij}}\phi(x)f_{ij}(x_{i})\mathbf{N}/z_{i}^{3}\frac{z_{i}^{3}}{\mathbf{N}^{T}\mathbf{d}_{i}}\mathbf{N}\mathrm{d}x_{i}\\&=\sum_{i,j}\int_{\Omega_{ij}}\phi(x)f_{ij}(x_{i})/(\mathbf{N}^{T}\mathbf{d}_{i})\mathbf{N}\mathrm{d}x_{i}\end{aligned}$$

保持 surface 本身的平滑性（对曲率进行约束）：

$$\operatorname{E}_{\mathrm{fair}}(S)=\int_{S}(\kappa_{1}^{2}+\kappa_{2}^{2})\mathrm{d}S$$

得到最终梯度：

$$\nabla E(x)=\nabla E_{\mathrm{erior}}(x)+{\nabla E_{\mathrm{fair}}(x)}$$