【笔记】基于图像的三维重建——表面重建

本文主要关于深蓝学院系列课程——基于图像的三维重建的笔记。

课程链接 基于图像的三维重建

1、三维物体的表面表达方式

边界表示法（Boundary Representation）： 将物体表面表示成一组封闭物体空间的四边形、三角形、参数曲面或者非参数的曲面，具有稳定性强、灵活性强、有助于表示表面细节。

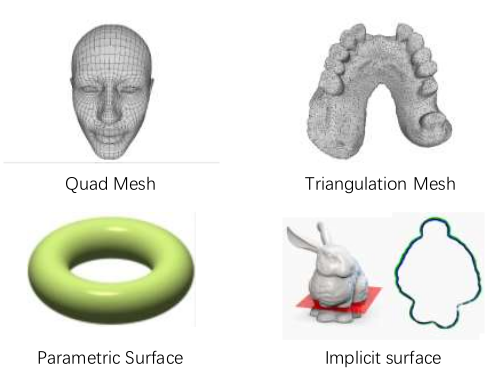
空间划分法（Spatial-Partitioning Representations）： 将物体内部的空间划分成细小、不重叠的连续实体来描述物体的形状。

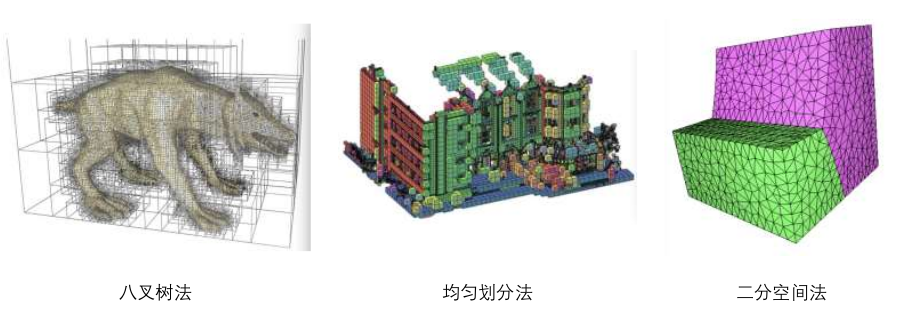
构造体素法（Boundary Constructive Solid Geometry）： 通过集合运算（并、交、差）将简单规则的形状组合成更加复杂的形状，操作简单、便于实现，但是只能用来表示较为简单的实体，无法用于形状复杂或者表面精细的物体。

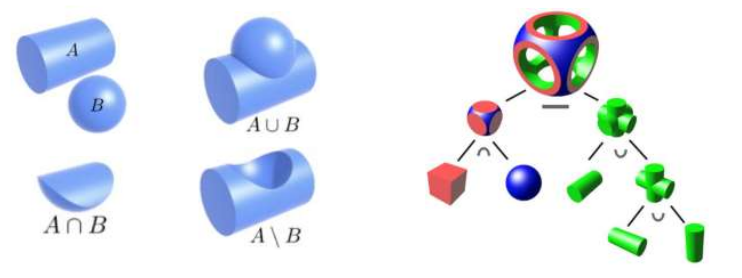
三角网格（Triangular Mesh）： 最常见的三维模型表述方式。计算机图形学和计算机视觉中的三维网格处理绝大部分都是基于三角网格。

• 三角网格的基本结构：
  • 顶点（Vertex）
  • 面片（Facet）
  • 边（Edge）
• 点线和面上的各种属性
  • 颜色（Color）
  • 法向量（Normal）
  • 纹理坐标（Texture Coordinate）

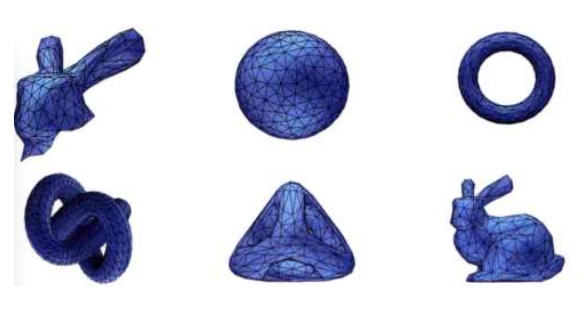
2、基于符号距离场的表面重建方法

2.1、基本概念

符号距离函数（Signed Distance Function）： 符号距离函数Signed Distance Function是某度量空间 $X$ 中的一个集合 $\Omega $ 的函数，决定 $X$ 中任一点到 $\Omega$ 边界 $\partial\Omega $ 的距离，并且由 $x$ 是在 $\Omega $ 内还是 $\Omega $ 外确定 SDF 的正负号：当 $x$ 在 $\Omega $ 内时，SDF 为正； 当 $x$ 在 $\Omega $ 外时， SDF 为负。

$$F(x)=\begin{cases}d(x,\partial\Omega)&ifx\in\Omega_i\\-d(x,\partial\Omega)&ifx\in\Omega_o\end{cases}$$

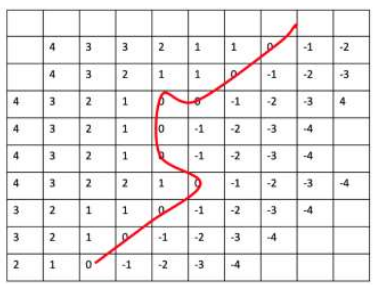
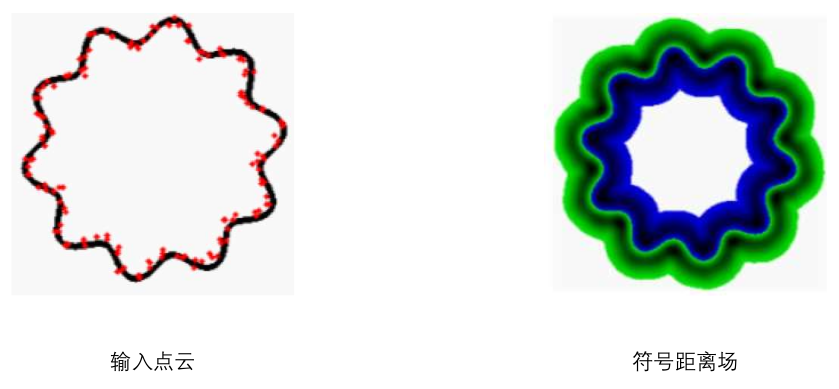
2.2、基于隐函数的表面重建

空间划分： 主要用于对隐函数进行离散化，即划分区域的每个区域计算一个符号距离值。

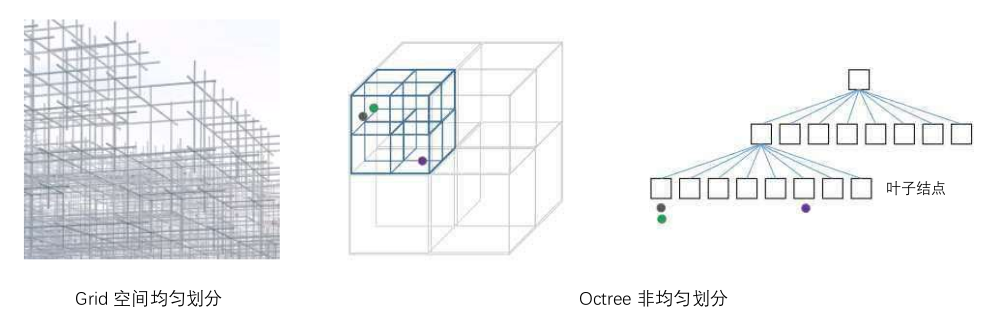
八叉树构建：

1. 设定最大递归深度；
2. 找出场景的最大尺寸，并以此尺寸建立第一个立方体；
3. 依序将元素丢入能被包含且没有子节点的立方体；
4. 若没达到最大递归深度，就进行细分八等份，再将该立方体所装的元素全部分给八个子立方体；
5. 若发现子立方体所分配到的元素数量不为零且跟父立方体是一样的，则该子立方体停止细分；
6. 重复3，直到达到最大递归深度。

符号距离场构建：

• 对于grid，根据邻域中的样本点计算每个node的符号距离；
• 对于octree，根据邻域中的样本点计算每个叶子结点的符号距离值。

符号距离场构建——局部方法：

符号距离场函数的一般定义：

$$F(\boldsymbol{x})=\frac{\sum_ic_iw_i(\boldsymbol{x})f_i(\boldsymbol{x})}{\sum_ic_iw_i(\boldsymbol{x})}$$

一种简单的情况：

$$\begin{aligned}f_i(x)&=(x-p_i)\cdot n_i\\\\w_i(x)&=\exp(-||x-p_i||^2)\end{aligned}$$

FSSR方法的符号距离函数定义：

$$\begin{aligned}f(x_i)&=f_x(x)f_y(y)f_z(z)=\frac{x}{\sigma^42\pi}\cdot e^{\frac{-1}{2\sigma^2}(x^2+y^2+z^2)}\\\\f_x(x)&=\frac{x}{\sigma^2}e^{\frac{-x^2}{2\sigma^2}}\quad f_y(x)=f_z(x)=\frac{1}{\sigma\sqrt{2\pi}}e^{\frac{-x^2}{2\sigma^2}}\end{aligned}$$

$$\begin{array}{rcl}w(\boldsymbol{x}_i)&=&w_x(x)\cdot w_{yz}(\sqrt{y^2+z^2})\\\\w_x(x)&=&\begin{cases}\frac{1}{9}\frac{x^2}{\sigma^2}+\frac{2}{3}\frac{x}{\sigma}+1&x\in[-3\sigma,0)\\\frac{2}{27}\frac{x^3}{\sigma^3}-\frac{1}{3}\frac{x^2}{\sigma^2}+1&x\in[0,3\sigma)\\0&\mathrm{otherwise}\end{cases}\\\\w_{yz}(r)&=&\begin{cases}\frac{2}{27}\frac{r^3}{\sigma^3}-\frac{1}{3}\frac{r^2}{\sigma^2}+1&r<3\sigma\\0&\mathrm{otherwise}\end{cases}\\\\r&=&\sqrt{y^2+z^2}.\end{array}$$

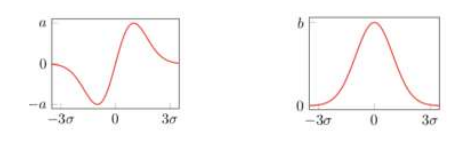
效果：

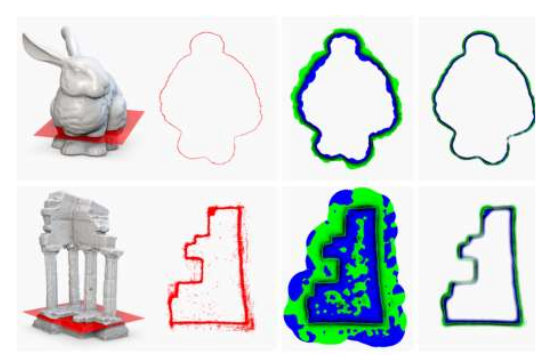
符号距离场的构建——全局方式： 将有向点看做是对隐函数的梯度的采样，全局的方法的 优点是鲁棒 ，能够很好地处理噪声和空洞，主要 缺点是计算量大 ，需要求解大规模的方程。

$$\begin{aligned} &\operatorname*{min}_{\chi_{M}}\|\nabla\chi_{M}-\vec{V}\| \\\\ &\nabla\cdot(\nabla\chi_{M})=\nabla\cdot\vec{V} \\\\ &\Delta\chi_{M} =\nabla\cdot\vec{\boldsymbol{V}} \\\\ &\chi_M(p)=\begin{cases}1&\text{if}p\in M\\0&\text{if}p\notin M\end{cases} \end{aligned}$$

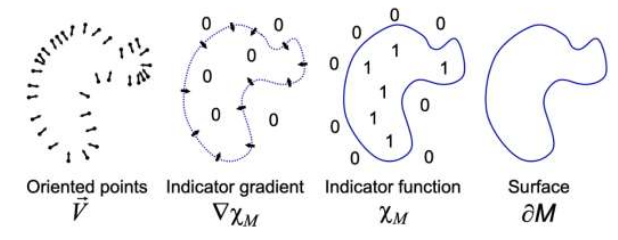
柏松表面重建方法：

1. 构建八叉树：

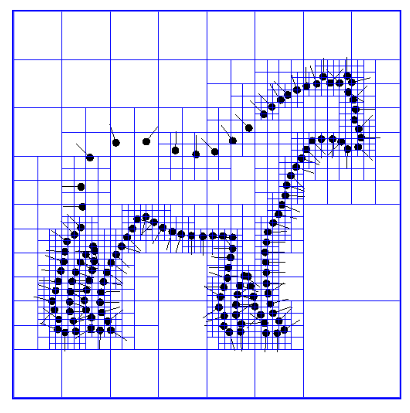
1. 创建向量场 $\vec{V}$ ：

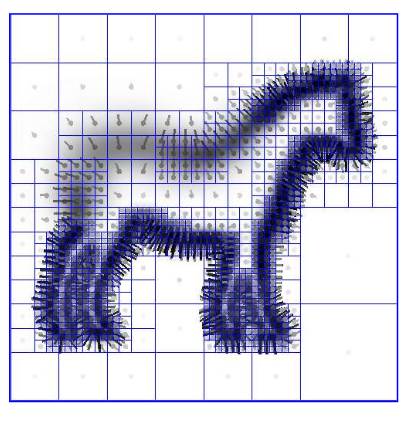
1. 计算指示函数 $\Delta\chi_{M} =\nabla\cdot\vec{\boldsymbol{V}}$：

不同分辨率下的指示函数表达：

1. 提取等值面：

Marching Cube 生成表面：

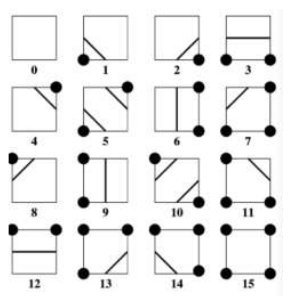
• 二维：根据四边形的 4个 顶点的符号距离值，通过插值的方法生成直线段。 总共 $2^4 =16$ 种分布状态。

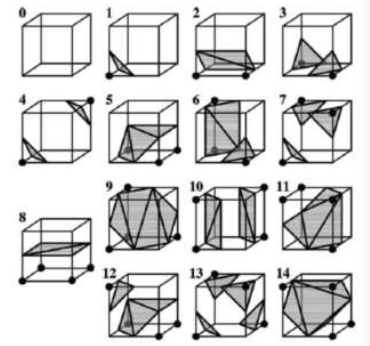
• 三维：通过插值法生成面片，共 $2^8 = 256$ 种分布状态，通过对称性可以简化成 15种 状态。

3、基于二元分割的表面重建方法

3.1、基本概念

主要思想： 将空间划分成一组 cell（voxel/tetrahedron），采用而远分割的思想，将这些 cell 划分成内部和外部两类，介于 interior 和 exterior 面，即为物体的 surface。

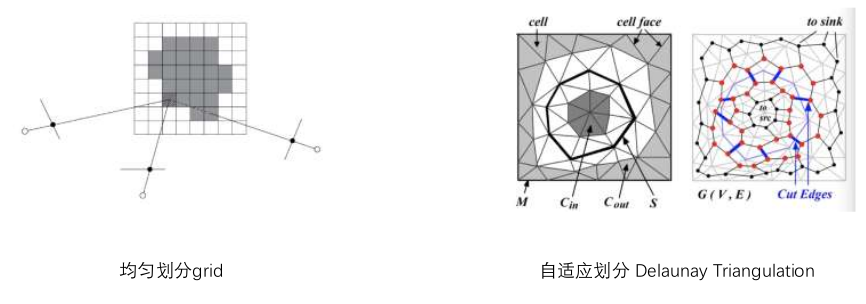
Delaunay Triangulation：

• 空圆特性：点集 $P$ 的德劳内三角剖分满足 $P$ 内任意一个点都不在 $P$ 内任意一个三角面片的外界圆内；任意 3个 点的外界圆不包含第 4个 点，即任意 3个 点的外界圆是空的；

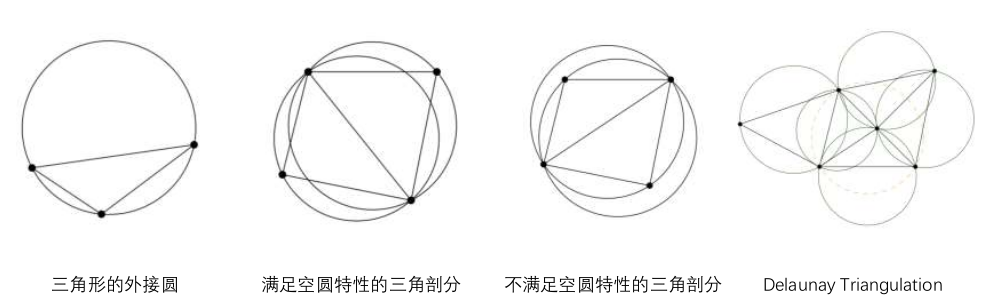
• 最大化最小角：德劳内三角剖分最大化三角面片内三角形的最小角。

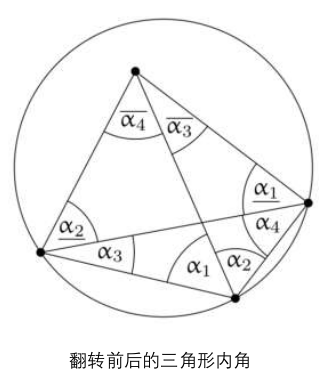
翻转前的内角： $\alpha_{1}+\alpha_{2},\quad\alpha_{3},\quad\alpha_{4},\quad\underline{\alpha_{1}},\quad\underline{\alpha_{2}},\quad\overline{\alpha_{3}}+\overline{\alpha_{4}}$ ；

翻转后的内角： $\alpha_{1},\quad\alpha_{2},\quad\overline{\alpha_{3}},\quad\overline{\alpha_{4}},\quad\underline{\alpha_{1}}+\alpha_{4},\quad\underline{\alpha_{2}}+\alpha_{3}$ ；

满足： 每一次翻转都是在增大三角剖分的最小角；

$$\begin{aligned} &&\alpha_{1}&& >\underline{\alpha_{1}}, \\ &&\alpha_2&& >\alpha_{2}, \\ &&\overline{\alpha_{3}}&& >\alpha_{3}, \\ &&\overline{\alpha_{4}}&& >\alpha_{4}, \\ &&\underline{\alpha_{1}}+\alpha_{4}&& >\alpha_{4}, \\ && \underline{\alpha_{2}}+\alpha_{3}&&>\alpha_{3} \end{aligned}$$

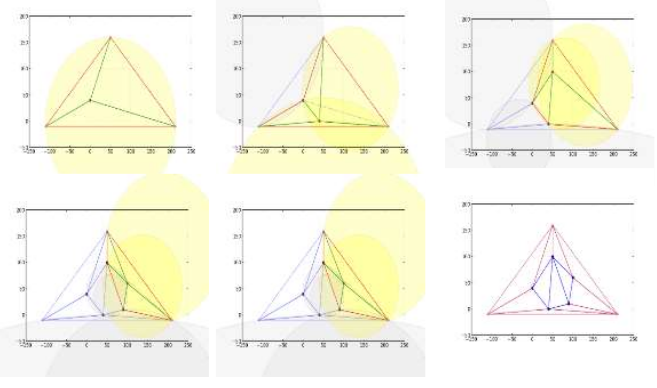
一种增量的德劳内三角剖分算法——Bowyer-Watson算法：

1. 假定已生成了链接若干个顶点的德劳内三角网络；
2. 加入一个新的节点，找出所有外界圆包含新加入节点的三角形，并将这些三角形删除，形成一个空腔。
3. 空腔的节点与新加入的节点连接，形成新的 Delaunay 三角形网络；
4. 不断循环直到遍历完所有点。

3.2、四面体剖分

四面体剖分： 3D 空间对应的是德劳内四面体剖分。在创建过程中，将点插入三角剖分前需要进行判断：

• 如果和已有的顶点距离较远，则直接插入新的顶点；
• 如果已经存在一个较近的顶点，则对该顶点进行更新。

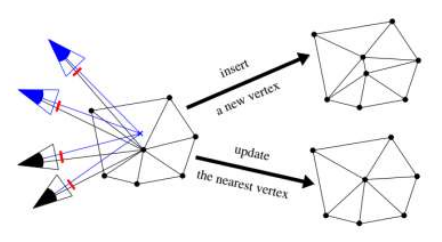
数学模型：

• 有向图的顶点对应四面体（tetrahedron），边界对应三角形（triangle）；
• 最小化下式将四面体划分成内部和外部两类：

$${ } E(S)=E_{vis}(S,P,v)+\lambda_{qual}E_{qual}(S)\\ \begin{aligned} &E_{vis}\colon\text{ 可视性代价}; \\ &E_{qual}\colon\text{ 表面质量代价}; \\ &S\colon\text{重建的表面;} \\ &P\colon{\text{点云;}} \\ &v\colon\text{ 摄像机位姿}; \end{aligned}$$

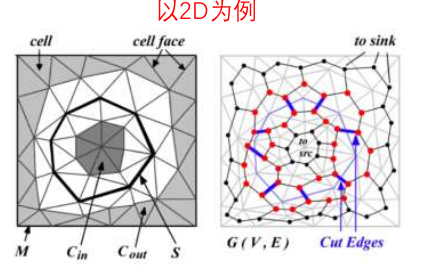
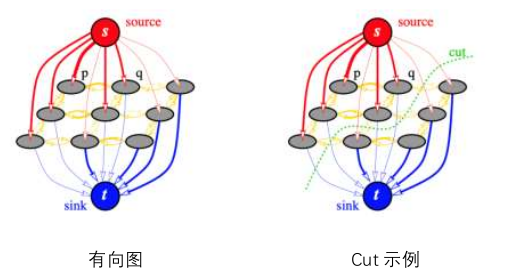
图割（Graph cut）：最大流（Max-flow）与最小割（Min-cut）：

• 有向加权图 $\mathcal{G}=\langle\mathcal{V},\mathcal{E}\rangle $ ，包含两个特殊的 terminal nodes： source 和 sink；
• 图割将所有节点 划分成没有交集的两部分，划分的代价定义为：

$$\mathfrak{c}(\mathcal{S},\mathcal{T})=\sum_{v_i\in\mathcal{S}\setminus\{s\}\atop v_j\in T\setminus\{t\}}w_{ij}+\sum_{v_i\in\mathcal{S}\setminus\{s\}}t_i+\sum_{v_i\in T\setminus\{t\}}s_i$$

可视性约束和局部平滑性的构建： 被 vertex 到相机中心的 ray 穿越的四面体倾向于 visible；

邻接表面可能存在的几种情况：外部-内部；内部-外部；外部-外部；内部-内部；

$$E_{vis}(S,P,v)=\sum_{p\in P}\sum_{q\in v_{p}}\left\{D_{out}\left(l_{\tau_{1}^{Q\rightarrow P}}\right)+\sum_{i=1}^{N_{[QP]}-1}V_{align}(l_{\tau_{l}^{Q\rightarrow P}},l_{\tau_{l+1}^{Q\rightarrow P}})+D_{in}(l_{\tau_{\mathcal{N}_{[QP]^{+1}}}^{Q\rightarrow P}})\right\}$$

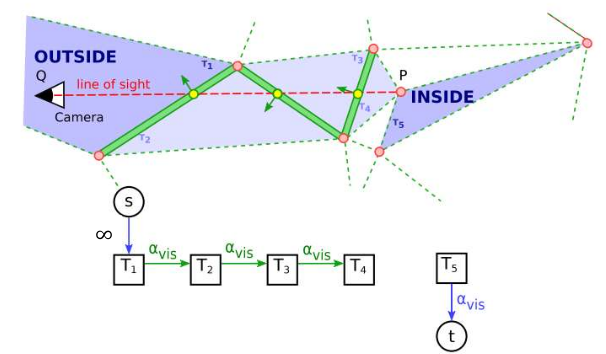
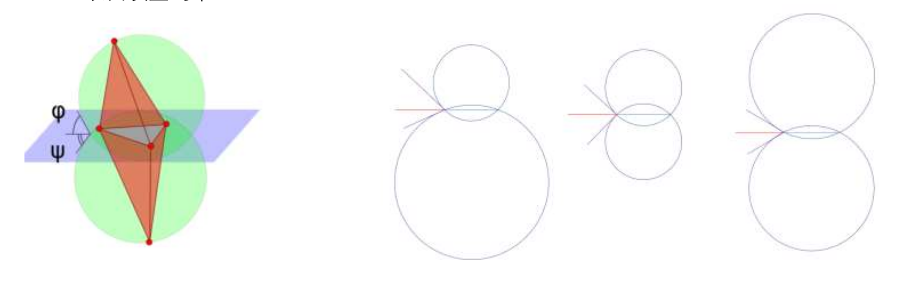
表面质量约束：

$$E_{qual}(s)=\sum_{f}w_{f}=1-\min\{\cos(\phi),\cos(\varphi)\}$$

总结：

• 算法流程简单，容易实现；
• 适用于大规模场景以及小物体的重建，能够处理复杂表面；
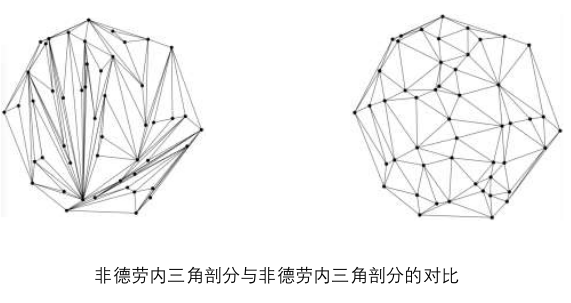
• 重建的效果以来 Delaunay Triangulation 的质量，容易受到噪声和外点的影响；
• 通常需要结合 Mesh refinement 获得更加细致的表面细节。

常用的重建算法：

• Delaunay Triangualtion + Graph Cut
• 泊松表面重建算法
• SSd 重建算法
• FSSR 重建算法