【笔记】基于图像的三维重建——稠密点云重建

本文主要关于深蓝学院系列课程——基于图像的三维重建的笔记。

课程链接 基于图像的三维重建

1、稠密点云的获取方式

• 主动式：
  • LiDAR扫描：精度高（毫米级别），效率高，有效范围几米到几百米，价格昂贵；受限于高反光、玻璃表面和吸收表面；
  • Kinect：使用方便，价格适中，速度较快；精度较低，有效距离短；
  • 结构光：高精度，高效率，近距离数据获取。
• 被动式：
  • Multi-view Stereo：无源被动式，成本低，图像来源广，计算速度慢，精度较高。

2、基于深度图的多视图立体几何

2.1、基础知识

像素点以及其对应的三维点之间的坐标关系：

• 像素点与相机坐标系下的三维点坐标关系：

$$\begin{aligned}&\boldsymbol{q}={\begin{pmatrix}\alpha&0&c_x&0\\0&\beta&c_y&0\\0&0&1&0\end{pmatrix}}\begin{pmatrix}\mathrm{x}_C\\y_C\\z_C\\1\end{pmatrix}=\boldsymbol{M}_i\boldsymbol{P}_c\\\\&\boldsymbol{q}={\begin{pmatrix}\alpha&0&c_x\\0&\beta&c_y\\0&0&1\end{pmatrix}}\begin{pmatrix}\mathrm{x}_C\\y_C\\z_C\end{pmatrix}=\boldsymbol{K}_i\widetilde{\boldsymbol{P}}_c \\\\ \end{aligned}$$ $$\boldsymbol{p}=\begin{pmatrix}u\\v\\1\end{pmatrix}=\frac{1}{z}{\begin{pmatrix}\alpha&0\\0&\beta&c_y\\0&0&1\end{pmatrix}}\begin{pmatrix}X_C\\y_C\\z_C\end{pmatrix}=\frac{1}{z}\boldsymbol{K}_i\widetilde{\boldsymbol{P}}_c\\\\ \tilde{\boldsymbol{P}}_{c}=\lambda\boldsymbol{K}_{i}^{-1}\boldsymbol{p}$$

• 像素点与世界坐标系下的三维点的坐标关系：

$$\begin{aligned}\widetilde{\boldsymbol{P}}_c&=\boldsymbol{R}_i\widetilde{\boldsymbol{P}}+\boldsymbol{T}_i\\\\\widetilde{\boldsymbol{P}}&=\boldsymbol{R}_i^\mathrm{T}\widetilde{\boldsymbol{P}}_c-\boldsymbol{R}_i^\mathrm{T}\boldsymbol{T}_i\end{aligned}$$

相机坐标原点与世界坐标系的关系：

$$\\\begin{pmatrix}0\\0\\0\end{pmatrix}=\boldsymbol{R}_i\boldsymbol{C}_i+\boldsymbol{T}_i\quad \\\\\boldsymbol{C}_i=-\boldsymbol{R}_i^\mathrm{T}\boldsymbol{T}_i$$

最终得到：

$$\widetilde{P}=R_{i}^{\mathrm{T}}\widetilde{P}_{c}+C_{i} \\\\ \widetilde{\boldsymbol{P}}=\lambda R_{i}^{\mathrm{T}}K_{i}^{-1}\boldsymbol{p}+C_{i}$$

面片模型：

概念：面片是三维物体表面的局部切平面，可以近似地表示某一局部范围内的物体表面。

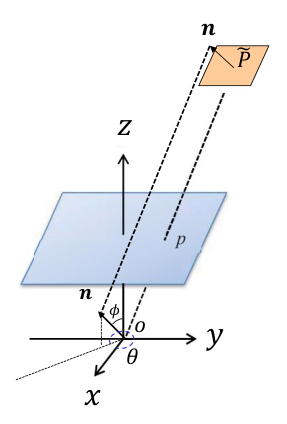
表示：面片 $p$ 是三维和空间中的一个矩形，由中心点 $\widetilde{P}$ 、单位法向量 $\boldsymbol{n}$ 表示，记作 $\boldsymbol{f_p=\{\widetilde{P} ,n\}}$

$$\widetilde{P}=\lambda R_{i}^{T}K_{i}^{-1}\boldsymbol{p}+C_{i} \\\\ \boldsymbol{n}_i=\begin{bmatrix}cos\boldsymbol{\theta}sin\boldsymbol{\phi}\\sin\boldsymbol{\theta}sin\boldsymbol{\phi}\\cos\boldsymbol{\phi}\end{bmatrix}$$

确定：面片由 $\lambda、\theta、\phi$ 决定，且一般限定范围为：

$$\lambda\in[\lambda_{min},\lambda_{max}],\theta\in[0^{\circ},360^{\circ}],\phi\in[0^{\circ},60^{\circ}].$$

光度一致性：

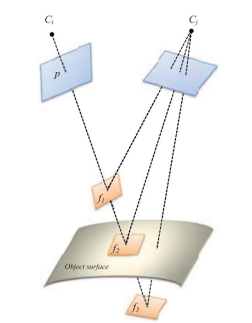
归一化相关系数：

$$NCC\big(\boldsymbol{q}_1,\boldsymbol{H}_{ij}(\boldsymbol{q}_1)\big)=\frac{\sum_{j=1}^{w\times\boldsymbol{w}}\big(q_\mathrm{j}-\overline{\boldsymbol{q}}\big)\cdot\big(\boldsymbol{H}_{ij}(q_\mathrm{j})-\overline{\boldsymbol{H}_{ij}(q_\mathrm{j})}\big)}{\sqrt{\Sigma_{j=1}^{w\times\boldsymbol{w}}\big(q_\mathrm{j}-\overline{\boldsymbol{q}}\big)^2\sum_{j=1}^{w\times\boldsymbol{w}}\big(\boldsymbol{H}_{ij}(q_\mathrm{j})-\overline{\boldsymbol{H}_{ij}(q_\mathrm{j})}\big)^2}}$$

其中 $H_{ij}$ 为相机 $i,j$ 的单应矩阵。

光度一致性函数：

$$m(p,\boldsymbol{f}_p)=1-NCC(\boldsymbol{q}_1,\boldsymbol{H}_{ij}(\boldsymbol{q}_1))$$

2.2、基于深度图的重建流程

核心重建步骤：

1. 立体对选择
2. 深度图计算
3. 深度图细化
4. 深度图融合

立体对选择：

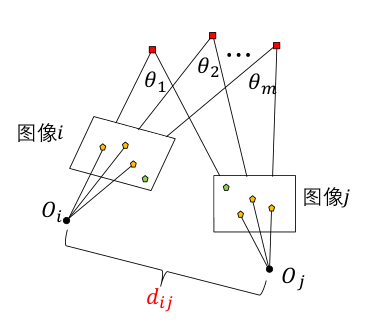
1. 计算平均角度值： $m$ 为图像 $i,j$ 在 SfM系统中建立的对应点个数：

$${\theta_{ij}}=\frac{1}{m}\sum_{k=1}^{m}\theta_{k}\quad\quad\quad{5^{\circ}}<\theta_{ij}<60^{\circ}$$

1. 计算基线距离： $\hat{d}$ 为所有 $d_{ij}, j=1,…,n$ 的中位数：

$${d_{ij}}>2\overline{d}\quad\quad d_{ij}<0.05\overline{d}$$

1. 按照 ${\theta_{ij}\cdot d_{ij}}$ 值的升序排列，选前 $k_1$ 个构建图像 $i$ 的邻域几何 $N(i)$ ；（升序是为了防止视距缩短以及遮挡问题）
2. 参考帧为 $N(i)$ 中 ${\theta_{ij}\cdot d_{ij}}$ 最小的图像。

深度图计算：

如果迭代次数小于等于 $k_2(\text{如：}k_2=3)$ ，则对于图像 $i$ 的每个像素进行如下操作：

• 空间传播：判断邻域像素的面片参数是否更优（即光度一致性的值是否更低）。如果更优，利用邻域像素的面片参数设置当前像素的面片参数；

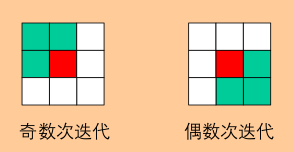
• 随机分配：通过随机采样，寻找光度一致性的值更低的面片参数。
  • 若给定三个值 $\{\Delta\lambda,\Delta\theta,\Delta\phi\}$ ，在范围 $\lambda^{\prime}\in(\lambda-\Delta\lambda,\lambda+ \Delta\lambda),\theta^{‘}\in(\theta-\Delta\theta,\theta+\Delta\theta),\phi^{‘}\in(\phi-\Delta\phi,\phi+\Delta\phi)$ 中随机选择一组平面参数 $\{\lambda^{\prime},\theta^{\prime},\phi^{\prime}\}$ ；
  • 使用公式 $\boldsymbol{X}_{i}=\lambda\boldsymbol{K}_{i}^{-1}\boldsymbol{p}、\boldsymbol{n}_{i}=\begin{bmatrix}cos\theta sin\phi\\sin\theta sin\phi\\cos\phi\end{bmatrix}$ ，重新计算新的平面 $f_{p}^{\prime}$ ；
  • 如果 $m(p,f_{p}^{\prime})<m(p,f_{p}),\text{则令：}f_{p}=f_{p}^{\prime},\lambda=\lambda^{\prime},\theta=\theta^{\prime},\phi=\phi^{\prime}$ ；
  • 将范围 $\{\Delta\lambda,\Delta\theta,\Delta\phi\}$ 减半；
  • 如果迭代次数小于等于制定次数 $k_3$ ，则回到第一步；否则，退出。

深度图细化：

1. 剔除光度一致性所有光度一致性高于 $\tau_1$ 的重建点；

2. 假设 $N_k$ 是 $N(i)$ 中的第 $k$ 个相邻图像，使用 $d(X,N_k)$ 表示 $X$ 相对相机 $N_k$ 的深度，$\lambda(X,N_k)$ 表示将 $X$ 投影到 $N_k$ 的深度图上得到的投影处的深度值：

   1. 如果 $\lambda(X,N_k)$ 与 $d(X,N_k)$ 足够接近，则认为两者具有深度一致性， $\tau_2$ 为阈值： $$\frac{|d(X,N_k)-\lambda(X,N_k)|}{\lambda(X,N_k)}<\tau_2$$
   2. 如果 $X$ 与 $N(i)$ 中至少 $k_4$ 张图像是一致的，则认为该点是可靠的，否则从 $I_i$ 的深度图中删除像素 $p$ 。

深度图融合：

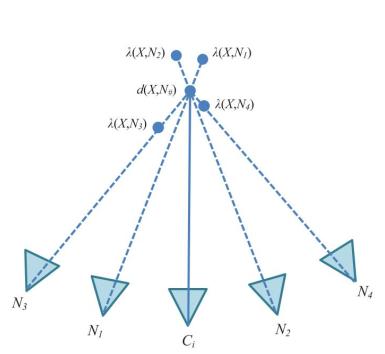
• 剔除：在邻域视图中，剔除被遮挡的像素，如 $N_1,N_2$ 图像中的像素点；
• 去冗余：在邻域视图中，融合深度值相近的像素，如 $N4$ 图像中的像素点；
• 深度图融合： $\widetilde{X}=\lambda R_{i}^{T}K_{i}^{-1}\boldsymbol{p}+\boldsymbol{C}_{i}$ 。

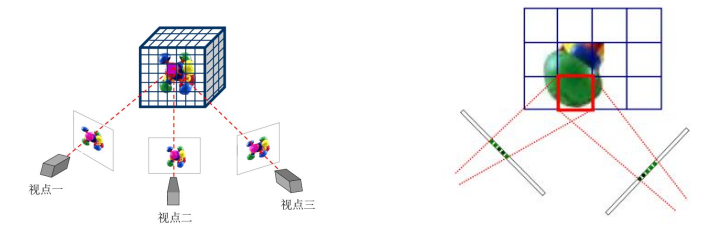
3、基于体素的多视图立体几何

体素重建： 基于体素的方法需要已知相机的内、外参数矩阵！！！

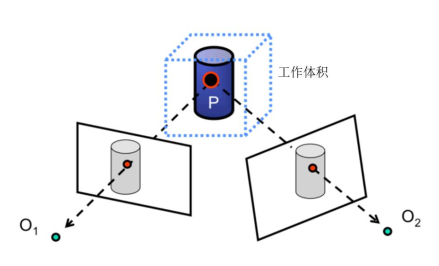
• 假设给定的工作体积包含待重建物体；
• 将工作体积内的三维点 $P$ 投影到多个视点的图像上；
• 验证 $P$ 点在各个视图上的投影点的“一致性”，以确定点 $P$ 是否属于待重建的物体。

3.1、空间雕刻法

基本概念：

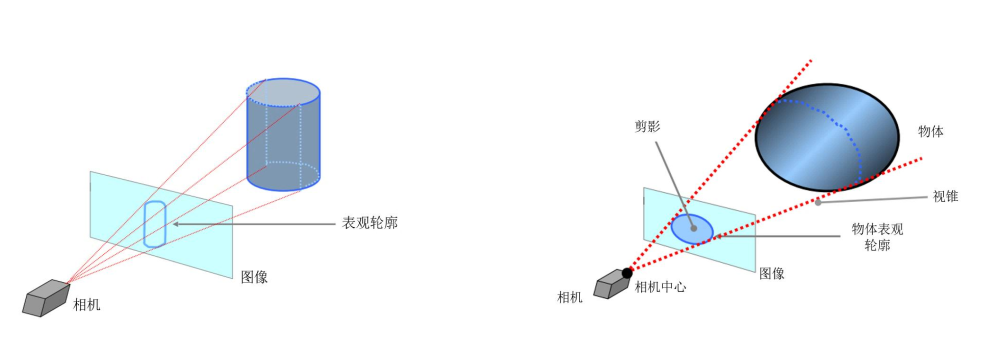
• 表观轮廓：物体表面可见部分和遮挡部分的分界线在图像平面上的投影。
• 剪影：图像平面中由表观轮廓包围的区域。
• 视锥：由相机中心和图像平面中对象的表观轮廓定义的包络面（待重建物体完全位于视锥内）。

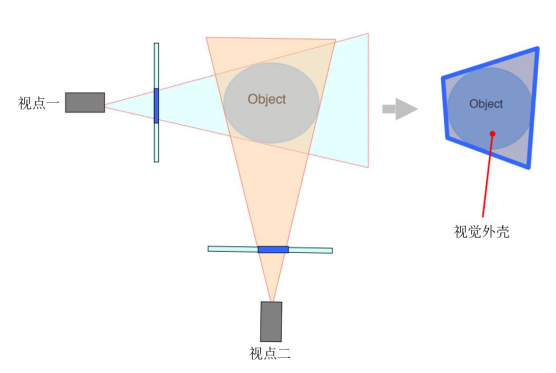
视觉外壳计算：

视觉外壳概念：艘有视锥的相交区域，它是待重建物体形状的逼近。

视觉外壳计算：对每个视锥建立参数方程，然后连理参数方程求解视锥交集，但过于复杂。

空间雕刻法的“一致性”定义： 给定工作体积中的一个点，将其投影到某个视图上时，如果投影点罗在该视图的剪影内，则称当前点满足该视图一致性要求。

空间雕刻法具体实现：

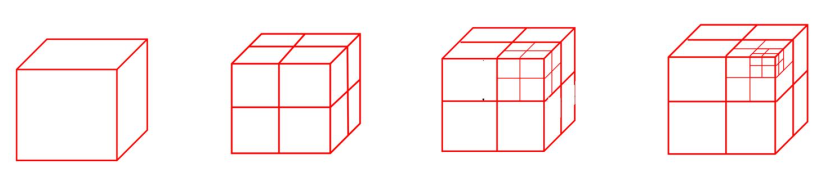
1. 将工作体积（立方体）分解为子体积（子立方体），也称为体素；
2. 评估所有体素：将待判定的体素投影到所有视点的图像中，只要有一个视图不满足一致性要求，即投影点在视图的剪影外，则将该体素标记为空；否则标记为满（红色）；
3. 得到所有相机视锥交集的近似估计。

注意：剪影法获得的视觉外壳是待重建物体形状的一个上限估计，即重建物体的任何部分都在外壳内，但外壳内的某些部分可能不属于物体。

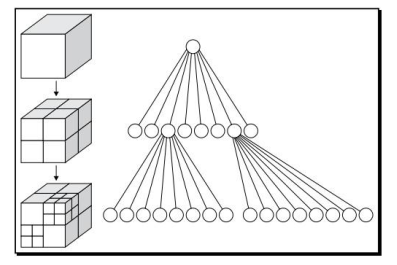
复杂度及解决： 采用上述方法对每个体素进行一致性估计，其计算复杂度太高，因此引入 八叉树 来解决。

八叉树： 基于八叉树的空间雕刻法，能在提高重建精度的同时，尽量减少计算复杂度。

空间雕刻法优缺点：

• 优点：
  • 简单且具有鲁棒性；
  • 不需要计算视图之间对应点的关系。
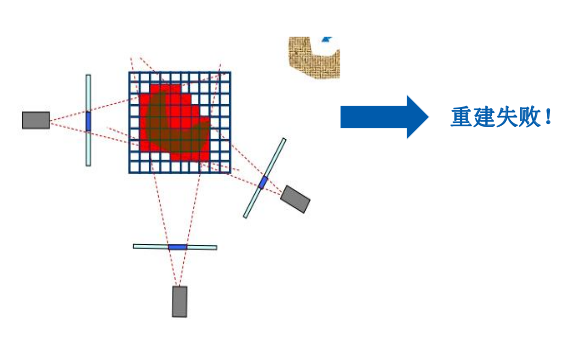
• 缺点：
  • 对视图数量的依赖；
  • 无法对物体的凹面进行建模。

3.2、体素着色法

体素着色法中的一致性： 使用投影点的色彩值来计算外观一致性。

计算步骤： 工作体积中的每个体素都被投影到图像中，因为体素具有一定的物理尺寸，所以它的投影很可能包含多个像素；计算这些像素的标准差，直接将其与某个阈值 $\lambda$ 比较来确认一致性。

色彩赋予： 对于那些通过外观一致性检测的体素，可以将其在图像上的投影点的色彩赋予它。

注意： 体素着色法仅适用于朗伯表面的重建任务，重建物体各个位置的感知亮度不随视点位姿变化而改变。

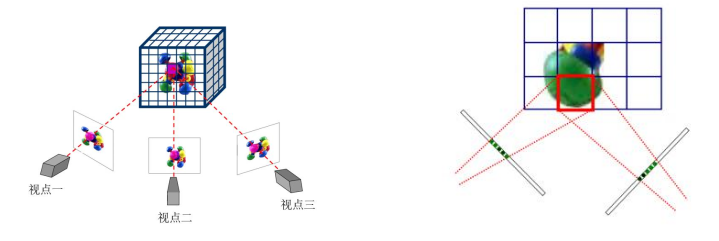
解决不唯一性问题的有效途径之一： 引入可见性约束，即遵循特定的顺序便利体素以消除歧义。

执行过程： 逐层探索体素一致性，从靠近相机的那些体素开始，然后逐渐到远离相机的那些体素。按照这个顺序，对每个体素执行一致性检查，并相应地将体素标记为满（占用）或者空（为占用）。