【笔记】基于图像的三维重建——运动恢复结构

本文主要关于深蓝学院系列课程——基于图像的三维重建的笔记。

课程链接 基于图像的三维重建

1、运动恢复结构问题

运动恢复结构问题（Structure from Motion, SfM）: 通过三维场景的多张图像，恢复出该场景的三维结构信息以及每张图片对应的摄像机参数。

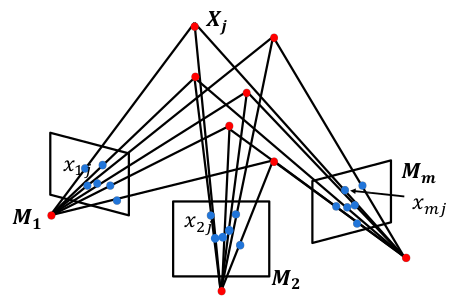
已知： $n$ 个 3D 点 $X_j$ 在 $m$ 张图像中的对应点的像素坐标 $x_{ij}(i=1,…,m;j=1,…,n)$ ，且 $x_{ij}=M_{i}X_{j}=K_{i}[R_{i}T_{i}]X_{j}\quad (i=1,…,m;j=1,…,n)$

求解：

• 运动： $m$ 个相机投影矩阵 $M_i(i=1,…,m)$ ；
• 结构： $n$ 个三维点 $X_j(j=1,…,n)$ 的坐标。

三类典型运动恢复结构任务：

• 欧式结构恢复（相机内参已知，外参未知）；
• 仿射结构恢复（相机为放射相机，内、外参均未知）；
• 透视结构恢复（相机为透视相机，内、外参数均未知）。

2、欧式结构恢复

2.1、双视图情况分析

已知：

• $n$ 个 3D 点 $X_j$ 在 $m$ 张图像中的对应点的像素坐标 $x_{ij}(i=1,…,m;j=1,…,n)$ ，且 $x_{ij}=M_{i}X_{j}=K_{i}[R_{i}T_{i}]X_{j}\quad (i=1,…,m;j=1,…,n)$
• $m$ 张图像对应的相机内参矩阵 $K_i(i=1,…n)$

求解：

• $n$ 个三维点 $X_j(j=1,…,n)$ 的坐标；
• $m$ 个相机外参数 $R_i,T_i(i=1,…,m)$。

三角化与欧式结构恢复： 两者仅相差相机外参数 $R_i,T_i$

• 线性法：

$$\begin{cases}x_{1j}=\boldsymbol{M_{1}X_{j}}=\boldsymbol{K_{1}[I\quad \mathbf{0}]X_{j}}\\\\x_{2j}=\boldsymbol{M_{2}X_{j}}=\boldsymbol{K_{2}[R\quad T]X_{j}}\end{cases}$$

• 非线性法：

$$X_{j}^{*}=\underset{x_{j}}{\mathrm{argmin}}\big(d\big(x_{1j},M_{1}X_{j}\big)+d(x_{2j},M_{2}X_{j})\big)$$

欧式结构恢复（2视图）求解步骤：

1. 求解基础矩阵 $F$ （归一化八点法）；
2. 求解本质矩阵 $E=K_2^T F K_1$ ；

$$\begin{aligned}&F={K^{\prime}}^{-T}[T_{\times}]RK^{-1}={K^{\prime}}^{-T}EK^{-1}\\\\&E=T\times R=[T_{\times}]R\end{aligned}$$

1. 分解本质矩阵 $E \to R、T$ ；
2. 三角化。

2.2、本质矩阵分解

目标：将本质矩阵 $E$ 分解为旋转和平移两个组成部分：

$$E=T\times R=[T_{\times}]R$$

符号、尺度不确定说明： $x_{2}^{T}Fx_{1}=0$ 中无法确定 $F$ 的符号和尺度，故 $E=K_{2}^{T}FK_{1}$ 也无法确定其符号和尺度。

定义矩阵：

$$W=\begin{bmatrix}0&-1&0\\1&0&0\\0&0&1\end{bmatrix}\quad\mathbf{Z}=\begin{bmatrix}0&1&0\\-1&0&0\\0&0&0\end{bmatrix}$$

上述矩阵 在相差一个正负号的情况下 有如下性质：

$$\mathbf{Z}=\mathrm{diag}(1,1,0)W=\mathrm{diag}(1,1,0)\boldsymbol{W}^{T}$$

$[T_x]$ 可以写成 $[T_\times]=kUZU^T$ ，其中 $U$ 是单位正交矩阵，在不考虑符号和尺寸的情况下 ：

$$[T_\times]=UZU^T=U\operatorname{diag}(1,1,0)WU^T=U\operatorname{diag}(1,1,0)W^TU^T$$

则：

$$\begin{aligned}E&=[T_\times]R\\&=(U\text{diag}(1,1,0)WU^T)R\\&=U\text{diag}(1,1,0)(WU^TR)\end{aligned}$$

对 $E$ 进行 SVD 分解：

$$E=U\mathrm{diag}(1,1,0)V^{T}$$

结合式子（8）、（9）：

$$R=UWV^{T}\quad\mathrm{or} \quad UW^{T}V^{T}$$

注意： $E$ 的这个因式分解只保证了$UWV^{T}、UW^{T}V^{T}$ 是正交的。其为旋转矩阵还需要保证行列式的值为正：

$$R=(\det\boldsymbol{U}WV^{T})\boldsymbol{U}WV^{T}\quad\text{或}\quad(\det\boldsymbol{U}W^{T}V^{T})\boldsymbol{U}W^{T}V^{T}$$

对于 $T$ ：

$$T\times T=[T_{\times}]T=UZU^{T}T=0 \\ T=\pm u_{3}\left(U\text{的第三列}\right)$$

则一共有 4组 解：

$$\begin{cases}\boldsymbol{R}=(\det\boldsymbol{U}\boldsymbol{W}\boldsymbol{V}^T)\boldsymbol{U}\boldsymbol{W}\boldsymbol{V}^T&\boldsymbol{T}=\boldsymbol{u}_3\\\boldsymbol{R}=(\det\boldsymbol{U}\boldsymbol{W}\boldsymbol{V}^T)\boldsymbol{U}\boldsymbol{W}\boldsymbol{V}^T&\boldsymbol{T}=-\boldsymbol{u}_3\\\boldsymbol{R}=(\det\boldsymbol{U}\boldsymbol{W}^T\boldsymbol{V}^T)\boldsymbol{U}\boldsymbol{W}^T\boldsymbol{V}^T&\boldsymbol{T}=\boldsymbol{u}_3\\\boldsymbol{R}=(\det\boldsymbol{U}\boldsymbol{W}^T\boldsymbol{V}^T)\boldsymbol{U}\boldsymbol{W}^T\boldsymbol{V}^T&\boldsymbol{T}=-\boldsymbol{u}_3\end{cases}$$

选择正确解：

• 选择一个点三角化，正确的一组解能保证该点在两个相机的 $z$ 坐标均为正；
• 对多个点进行三角化，选择在两个相机系下 $z$ 坐标均为正的个数最多的那组 $R、T$ 。（更鲁棒）

本质矩阵分解小结：

1. SVD分解：$E=U\mathrm{diag}(1,1,0)V^{T}$ ；
2. $R=(\det\boldsymbol{U}WV^{T})\boldsymbol{U}WV^{T}\quad\text{或}\quad(\det\boldsymbol{U}W^{T}V^{T})\boldsymbol{U}W^{T}V^{T}$ ；$T=\pm u_{3}\left(U\text{的第三列}\right)$ ；
3. 得到四组解：式子（13）；
4. 通过重建单个或者多个点找出正确解。

欧式结构恢复歧义：

• 歧义：恢复的结构与真实场景之间相差一个相似变换（旋转、平移、缩放）；
• 度量重构：恢复的场景与真实场景之间仅存在相似变换的重构。

2.3、N视图情况

代数方法：

• 增量法：分别对每一个图像对计算运动和结构

• 局限性：容易出现误差累积

捆绑调整（Bundle Adjustment，BA）：

最小化重投影误差：

$$E(M,X)=\sum_{i=1}^{m}\sum_{j=1}^{n_{i}}D(x_{ij},M_{i}X_{j})^{2}$$

方法：非线性最小化问题 ，牛顿法或L-M法

优势：

• 同时处理大量视图
• 处理丢失的数据

局限性：

• 大量参数的最小化问题
• 需要良好的初始条件

实际操作： 常用作 SfM 的最后一步，分解方法可作为优化问题的初始解。

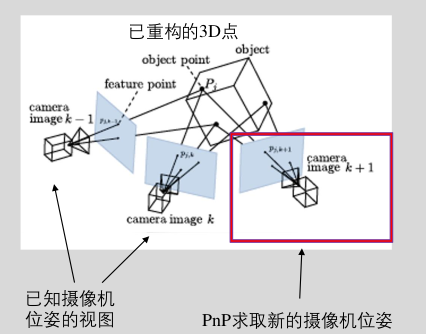
3、PnP问题与P3P方法

PnP（Perspective-n-Point）问题： 指通过世界中 $N$ 个三维点坐标及其在图像中 $N$ 个像点坐标，计算出相机或者物体位姿的问题。

P3P方法： 通过世界中的3个三维点与图像中的3个像点，计算摄像机的位姿。

已知：相机内参 $K$ ，像素平面上 $a,b,c$ 点的像素坐标以及其对应的三维点 $A,B,C$ 在世界坐标系中的世界坐标；

求解：相机外参 $R、T$ 。

求解思路：

1. 通过求解 $A,B,C$ 三点在当前相机坐标系下的坐标；
2. 通过 $A,B,C$ 在当前相机下的坐标以及其在世界坐标系下的坐标，估计摄像机相对于世界坐标系的旋转和平移。

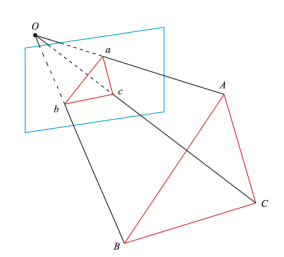
求解步骤：

1. 通过相机内参数求得 $\overrightarrow{oa},\overrightarrow{ob},\overrightarrow{oc}$ 三条直线的方向，并计算 $cos<\overline{oa},\overrightarrow{ob}>,\cos<\overrightarrow{ob},\overrightarrow{oc}>,cos<\overrightarrow{oa},\overrightarrow{oc}>$

由已知信息可得：

$$a=K(I,0)\begin{pmatrix}\widetilde{A}\\1\end{pmatrix}=K\widetilde{A} \\ \tilde{A}=K^{-1}a$$

则可得：

$$\begin{gathered} \overrightarrow{oa} =\frac{K^{-1}a}{\sqrt{\|K^{-1}a\|}} \\ \overrightarrow{ob} =\frac{K^{-1}b}{\sqrt{\|K^{-1}b\|}} \\ \text{oc} =\frac{K^{-1}c}{\sqrt{\|K^{-1}c\|}} \end{gathered}$$

求得：

$$\begin{gathered} cos<\overrightarrow{oa},\overrightarrow{ob}>=\overrightarrow{oa}\cdot\overrightarrow{ob} \\ cos<\overrightarrow{ob},\overrightarrow{oc}>=\overrightarrow{ob}\cdot\overrightarrow{oc} \\ cos<\overrightarrow{oa},\overrightarrow{oc}>=\overrightarrow{oa}\cdot\overrightarrow{oc} \end{gathered}$$

1. 通过三角函数，求解线段 $OA,OB,OC$ 长度：

$$\begin{aligned}OA^2+OB^2-2OA\cdot OB\cdot cos&<\overrightarrow{oa},\overrightarrow{ob}>=A\text{B}^2\\OB^2+OC^2-2OB\cdot OC\cdot cos&<\overrightarrow{ob},\overrightarrow{oc}>=\text{B}C^2\\OA^2+OC^2-2OA\cdot OC\cdot cos&<\overrightarrow{oa},\overrightarrow{oc}>=AC^2\end{aligned}$$

上述方程组存在四个可能解，需要另一对点对进行验证。

1. 结合 $OA,OB,OC$ 线段安长度可以得到 $A,B,C$ 在相机坐标系下的坐标；
2. 利用 $A,B,C$ 在相机坐标系及世界坐标系的坐标，计算相机的运动 $R,T$。

4、单应矩阵

单应矩阵： 空间平面在两个相机下的投影几何。

单应矩阵推导：

已知：两个相机内参矩阵分别为 $K,K’$ ，第二个相机相对于第一个相机的位姿为 $(R,T)$ ，$n$ 为平面 $\pi$ 在第一个相机坐标系下的单位法向量， $d$ 为坐标原点到平面 $\pi$ 的距离。

$$\begin{aligned}\boldsymbol{M}&=\boldsymbol{K}(\boldsymbol{I},0),\boldsymbol{M}^{\prime}=\boldsymbol{K}^{\prime}(\boldsymbol{R},\boldsymbol{T}),\boldsymbol{P}=\left(\vec{\boldsymbol{P}}^{\mathrm{T}},1\right)^{\mathrm{T}}\\\\\boldsymbol{p}&=\boldsymbol{M}\begin{pmatrix}\vec{\boldsymbol{P}}\\1\end{pmatrix}=\boldsymbol{K}\vec{\boldsymbol{P}}\quad\Longleftrightarrow\quad\widetilde{\boldsymbol{P}}=\boldsymbol{K}^{-\mathbf{1}}\boldsymbol{p}\\\\\boldsymbol{p}^{\prime}&=\boldsymbol{M}^{\prime}\begin{pmatrix}\vec{\boldsymbol{P}}\\1\end{pmatrix}=\boldsymbol{K}^{\prime}(\boldsymbol{R},\boldsymbol{T})\begin{pmatrix}\vec{\boldsymbol{P}}\\1\end{pmatrix}=\boldsymbol{K}^{\prime}(\boldsymbol{R}\widetilde{\boldsymbol{P}}+\boldsymbol{T})\\\\\boldsymbol{p}^{\prime}&=\boldsymbol{K}^{\prime}(\boldsymbol{R}\vec{\boldsymbol{P}}+\boldsymbol{T})=\boldsymbol{K}^{\prime}(\boldsymbol{R}-\boldsymbol{T}\boldsymbol{n}_d^{\mathrm{T}})\boldsymbol{\tilde{\boldsymbol{P}}}=\boldsymbol{K}^{\prime}(\boldsymbol{R}-\boldsymbol{T}\boldsymbol{n}_d^{\mathrm{T}}\boldsymbol{R}^{-\mathbf{1}}\boldsymbol{p}&\end{aligned}$$

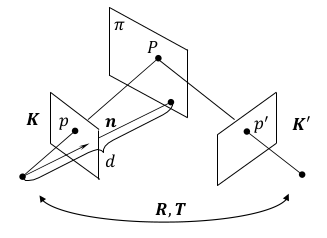
其中平面 $\pi$ 的方程为： $n^{T}\widetilde{\boldsymbol{P}}+d=0$

结论： 最终得到：

$$p^{\prime}=Hp\quad \\H=K^{\prime}(R-Tn_d^\mathrm{T})K^{-1}\\ \text{其中：} n_{d}=\frac{n}{d}$$

单应矩阵估计：

已知： $m$ 对点对应满足 $p’=Hp$ ；

求解：单应矩阵 $H$ 。

由已知可知：

$$\begin{pmatrix}x'\\y'\\w'\end{pmatrix}=\begin{pmatrix}h_1&h_2&h_3\\h_4&h_5&h_6\\h_7&h_8&h_9\end{pmatrix}\begin{pmatrix}x\\y\\w\end{pmatrix}$$

即：

$$\begin{aligned}u'&=\frac{x'}{w'}=\frac{h_1x+h_2y+h_3w}{h_7x+h_8y+h_9w}\\\\v'&=\frac{y'}{w'}=\frac{h_4x+h_5y+h_6w}{h_7x+h_8y+h_9w}\end{aligned}$$

不失一般性，令 $w=1$ ：

$$\begin{aligned}&u'(h_7u+h_8v+h_9)=h_1u+h_2v+h_3\\\\&v'(h_7u+h_8v+h_9)=h_4u+h_5v+h_6\end{aligned}$$

转化为矩阵形式：

$$\begin{bmatrix}-u_1&-v_1&-1&0&0&0&u_1u_1'&v_1u_1'&u_1'\\0&0&0&-u_1&-v_1&-1&u_1v_1'&v_1v_1'&v_1'\\-u_2&-v_2&-1&0&0&0&u_2u_2'&v_2u_2'&u_2'\\0&0&0&-u_2&-v_2&-1&u_2v_2'&v_2v_2'&v_2'\\&\vdots&&&\vdots&&&\vdots&\end{bmatrix} \begin{bmatrix}h_1\\h_2\\h_3\\h_4\\h_5\\h_6\\h_7\\h_8\\h_9\end{bmatrix}=0$$

即：

$$A\tilde{\boldsymbol{h}}=\mathbf{0}$$

8自由度的 $H$ 至少需要4对点对应，实际远多于4对点对应

基础矩阵与单应矩阵：

由：

$$\begin{aligned}&p^{\prime\text{T}} F p = 0 \\ \\ & p ^ { \prime }=Hp\end{aligned}$$

得到：

$$p^{\prime\text{T}} F H ^ { - 1 }p^{\prime}=0 \\ F=SH$$

• 其中 $S=[t_{\times}]$ ，$t$ 是任意向量，具有三个自由度。

• 只要 $FH^{-1} =S$ 其中 $S$ 为 $3\times3$ 的反对称矩阵，则式（80）成立。

• 给定空间中同一平面上任意多个的三维点，我们仅能得到 $F=SH$ ，即无法得到确定的 $F$ ，也就无法得到 $E$ ，则无法分解 $R,T$ 。

• 解决上面问题，我们采用分解单应矩阵求解 $R,T$ 。$H=K^{\prime}(R-Tn_d^\mathrm{T})K^{-1}$

本质矩阵、基础矩阵与单应矩阵：

• 表达：

  • 本质矩阵：$E=T\times R=[T_\times]R$ ；
  • 基础矩阵：$\begin{array}{c}F={K^{\prime}}^{-\mathrm{T}}[T_{\times}]RK^{-1}\\={K^{\prime}}^{-\mathrm{T}}EK^{-1}\end{array}$ ；
  • 单应矩阵：$H=K^{\prime}(R-Tn_d^\mathrm{T})K^{-1}$ ，$n^{\mathrm{T}}\widetilde{P}=d，n_{d}=\frac{n}{d}$

• 场景结构：

  • 本质矩阵：描述规范化相机下两视图间的对极约束与场景结构无关，其仅依赖相机间的旋转和平移；
  • 基础矩阵：描述两视图间的对极约束与场景结构无关，其仅依赖相机间的旋转和平移；
  • 单应矩阵：要求场景中的点位于同一平面；或者两个相机之间只有旋转而无平移；
• 约束关系：
  • 本质矩阵：建立规范化相机下点和极线的对应关系；
  • 基础矩阵：建立点和极线的对应关系；
  • 单应矩阵：建立点和点的对应关系。