本文主要关于深蓝学院系列课程——基于图像的三维重建的笔记。
课程链接 基于图像的三维重建
1、基于平行视图的双目立体视觉
平行视图: 平行视图为极几何的一种特例。
- 基线平行于图像平面,极点 $e$ 和 $e’$ 位于无穷远处;
- 极线是水平的,平行于 $u$ 轴;
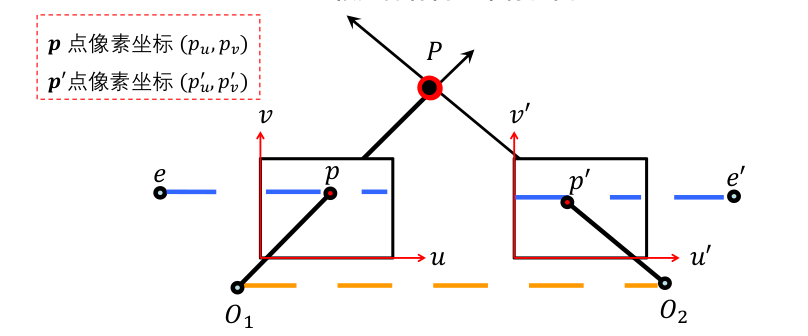
平行视图的基础矩阵:
$O_1$ 在右像素平面上的投影点为:
叉乘性质:对于任何向量 $a$ ,如果 $B$ 可逆,相差一个尺度情况下:
令 $a=T,B=K^{\prime{-1}}$ ,则:
根据基础矩阵 $F={K^{\prime}}^{-\mathrm{T}}[T_{\times}]RK^{-1}$ ,得到:
代入 (1)式可得:
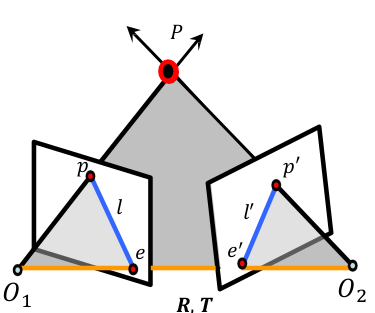
平行视图的极线 $l$ 为: 极线是 水平的,平行与 $u$ 轴 :
平行视图的 $p$ 和 $p’$ 关系: 两者 $v$ 坐标相同:
平行视图的性质:
- 极线是水平的,平行于 $u$ 轴;
- 极点位于无穷远;
- $p$ 和 $p’$ 的 $v$ 坐标一样
平行视图的三角测量:
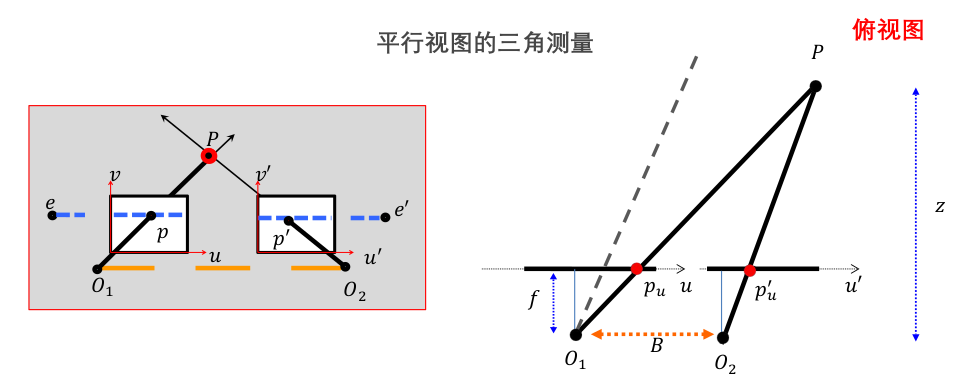
根据上图可得:
视差 $p_{u}-p_{u}^{\prime}$ 与深度 $z$ 成反比。
双目立体视觉系统构建的核心问题:
- 如何获得平行视图?
- 如何建立点对应关系?
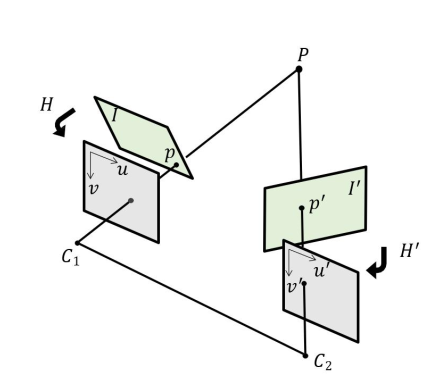
2、图像校正
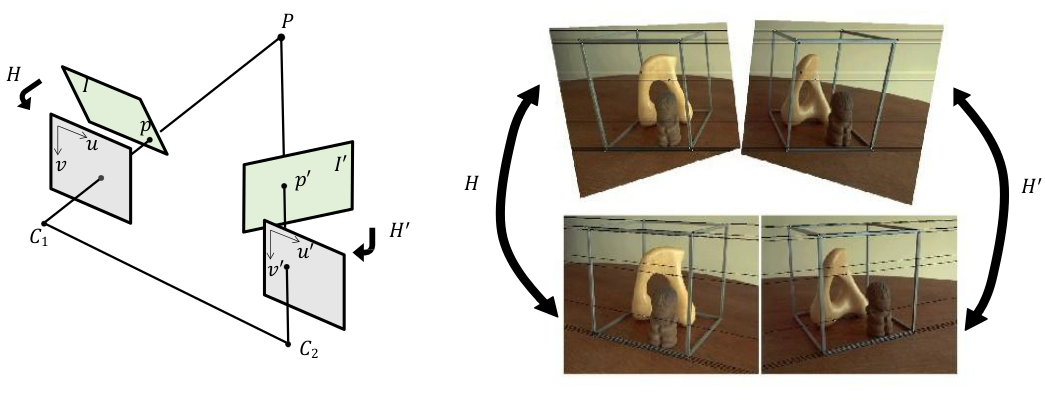
图像校正步骤:
- 在两副图像 $I$ 和 $I’$ 找到一组匹配点 $p_i \to p’_i$ ,不少于8个;
- 计算基础矩阵 $F$ ,求解两副图像中的极点 $e$ 和 $e’$ ;
- 选择透视变换 $H’$ 将 $e’$ 映射到无穷远点 $(f,0,0)$ ;
- $I’$ 的中心点的齐次坐标为$(0,0,1)$ ,$e’$ 的齐次坐标为 $(e’_1,e’_2,1)$ :
- $e’>0$ 时, $\alpha=1$ ,反之 $\alpha=-1$ ;$e’$ 的齐次坐标$(f,0,1)$ :
- $e’$ 的齐次坐标为$(f,0,0)$ :
- 寻找对应的透视变换矩阵 $H$ ,使得下式最小:
对上式解释:平行视图中,对应的极线方程是相同的:
已知:直线 $l$ 和变换矩阵 $H$ ;
求解:变换后的直线${\boldsymbol{\ell}}$
故要最小化 ${\boldsymbol{\ell}}$ 和 ${\boldsymbol{\ell}’}$ 等价于式(15)。
- 分别用矩阵 $H$ 和 $H’$ ,对左右两副图像 $I$ 和 $I’$ 进行重采样。
3、对应点搜索
双目融合问题: 给定 3D 点 $P$ ,在左右图像中找到相应的观测值 $p$ 和 $p’$ 。
平行视图的对应点搜索: 图像校正后, $p’$ 点沿着扫描线寻找即可。
归一化相关匹配:
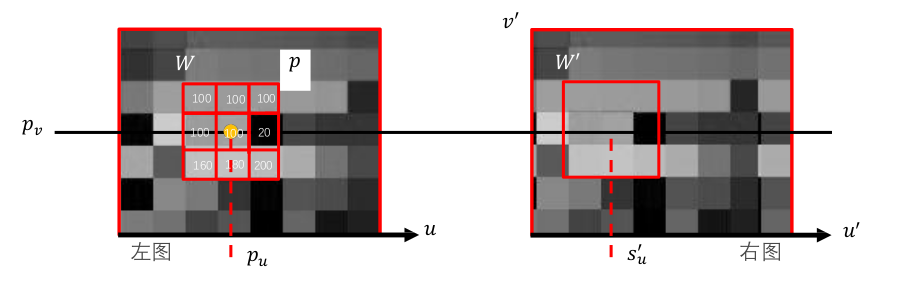
- $p=(p_u,p_v)$ 处选择一个窗口 $W$ ,建立向量 $w$ ;
- 在右图中沿扫描线在每个位置 $s’_u$ 建立窗口 $W’$ ,并获得 $w’$ 向量;
- 计算每个 $s’_u$ 位置的$\frac{(w-\overline{w})^\mathrm{T}(w^{\prime}-\overline{w}^{\prime})}{||w-\overline{w}||\times||(w^{\prime}-\overline{w}^{\prime})||}$ 的值; $\overline{w}$ 为向量中每个元素均为 $W$ 内的灰度均值,目的是消除亮度和曝光的影响。
- $p_{u}^{\prime}=arg\mathrm{max}\frac{(w-\bar{w})^{T}(w^{\prime}-\bar{w}^{\prime})}{||w-\bar{w}||\times||(w^{\prime}-\bar{w}^{\prime})||}$ 。
窗口大小的影响:
- 较小的窗口:细节丰富;噪声更多;
- 较大的窗口:视差图更平滑、噪声更少;细节丢失;

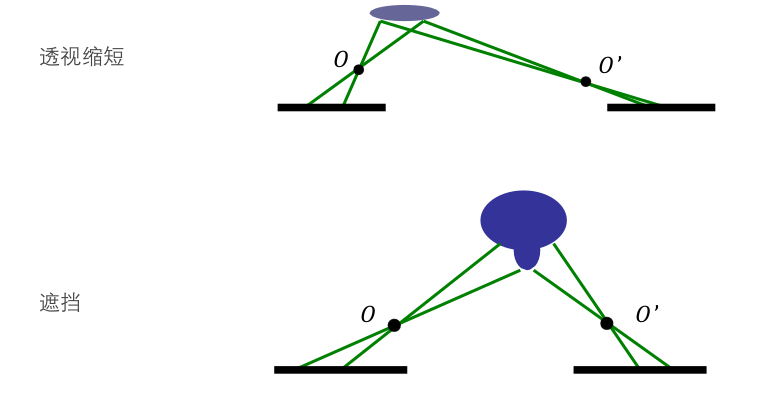
相关法存在的问题:
- 透视缩短
- 遮挡
- 基线选择
- 同质区域
- 重复模式


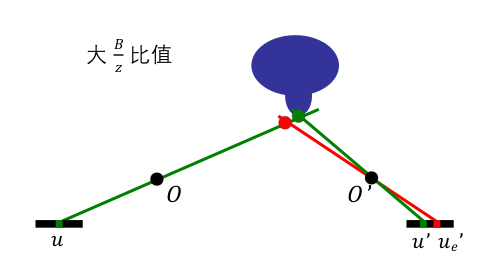
透视缩短和遮挡的解决方法: 为了减少透视缩短以及遮挡的影响,希望更小的 $B/z$ (基线深度比)比值,但当 $B/z$ 小时,测量值的小误差意味着估算深度的大误差。
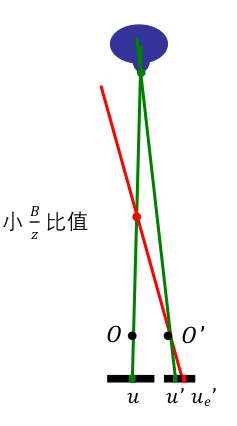
引入其他约束: 为解决相关法的缺陷问题,引入其他约束:
- 唯一性约束:一张图像中的任何点,在另一张图像中最多只有一个匹配点;
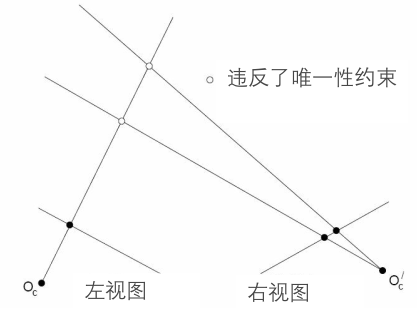
- 顺序约束/单调性约束:左右视图中的对应点次序一致:
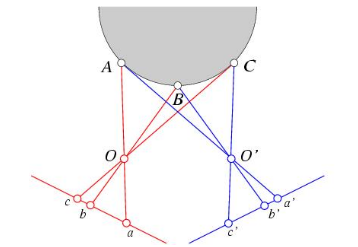
- 平滑性约束:视差函数通常是平滑的。