【笔记】基于图像的三维重建——图像特征

本文主要关于深蓝学院系列课程——基于图像的三维重建的笔记。

课程链接基于图像的三维重建

1、局部特征：角点

1.1、图像特征

特征提取动机： 全景拼接

全景拼接步骤：

特征提取
特征匹配
图像对齐

好特征的特性：

可重复性
显著性
紧致、高效
局部性

应用场景：

图像对齐
三维重建
运动跟踪
机器人导航
索引和数据库检索
物体识别

1.2、角点检测

基本思想： 角点处，向任何方向移动窗口，灰度都会发生很大变化。

关键性质： 角点附近的区域，图像梯度有两个或多个主方向。

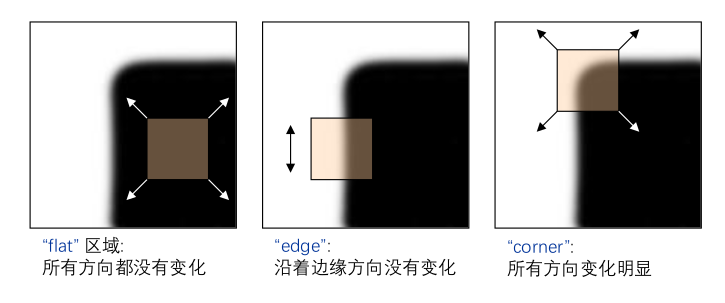
数学表达： 窗口 $w(x,y)$ 移动 $[u,v]$ 时的外观变化：

$E(u,v)=\sum_{x,y}w(x,y)\big[I(x+u,y+v)-I(x,y)\big]^2$

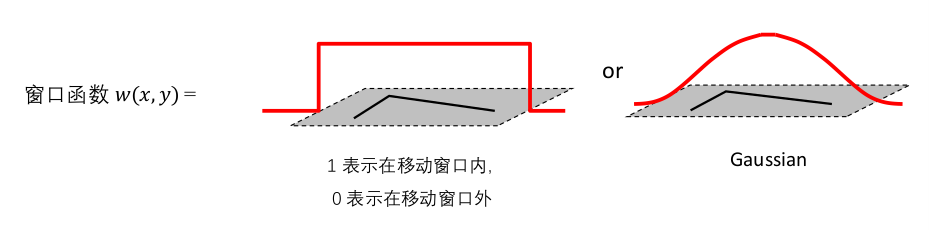
由于 $[u,v]$ 和 $E(u,v)$ 间存在 $I(x,y)$ 函数，无法反映两者之间关系，故对 $E(u,v)$ 在$(0,0)$ 处进行 二阶泰勒展开：

$E(u,v)\approx E(0,0)+\begin{bmatrix}u&v\end{bmatrix}\begin{bmatrix}E_u(0,0)\\E_v(0,0)\end{bmatrix}+\dfrac{1}{2}[u v]\begin{bmatrix}E_{uu}(0,0)&E_{uv}(0,0)\\E_{uv}(0,0)&E_{vv}(0,0)\end{bmatrix}\begin{bmatrix}u\\v\end{bmatrix}$

得到：

$E_{uu}(0,0)=\sum_{x,v}2w(x,y)I_{x}(x,y)I_{x}(x,y) \\ E_{vv}(0,0)=\sum_{x,v}2w(x,y)I_{y}(x,y)I_{y}(x,y) \\ E_{uv}(0,0)=\sum_{x,v}2w(x,y)I_{x}(x,y)I_{y}(x,y) \\ E(0,0)=0 \\ E_{u}(0,0)=0 \\ E_{v}(0,0)=0$

得到二阶近似表达：

$E(u,v)\approx(u \quad v)\boldsymbol{M}\binom uv \\ 其中，\quad M=\sum_{x,y}w(x,y)\begin{pmatrix}I_x^2&&I_xI_y\\I_xI_y&&I_y^2\end{pmatrix}$

二阶矩矩阵： 考虑 $E(u,v)$ 的一个水平切片，其几何形状是一个椭圆。

$E(u,v)\approx(u\quad v)\boldsymbol{M}\binom uv\Rightarrow(u\quad v)\boldsymbol{M}\binom uv=\text{常数}$

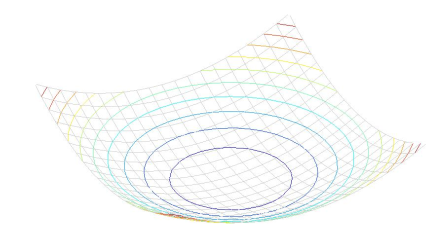
假设对角化矩阵 $M=R^{-1}\begin{pmatrix}\lambda_{1}&0\\0&\lambda_{2}\end{pmatrix}R$ ，其椭圆的轴长由特征值 $\lambda_{1},\lambda_{2}$ 决定，方向由矩阵 $R$ 决定。

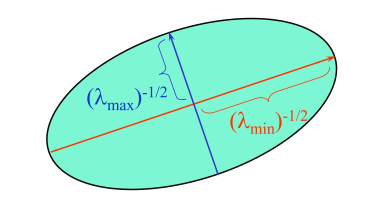
特征值： 利用二阶矩矩阵$M=R^{-1}\begin{pmatrix}\lambda_{1}&0\\0&\lambda_{2}\end{pmatrix}R$ 的特征值对图像中的点进行分类：

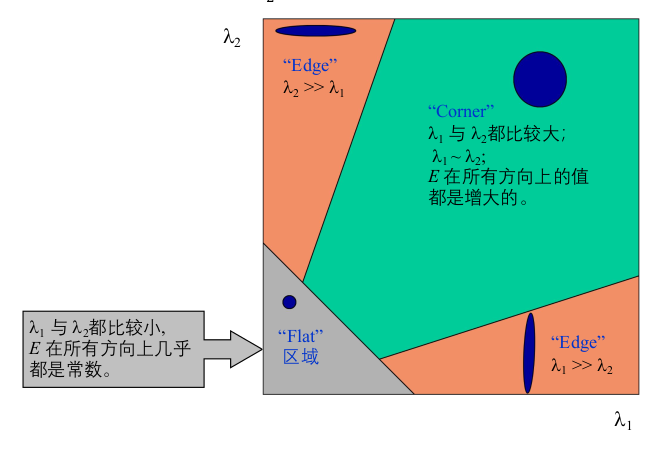
角点响应函数：

$\mathcal{R}=\det(M)-\alpha\text{trace}(M)^2=\lambda_1\lambda_2-\alpha(\lambda_1+\lambda_2)^2 \\ \alpha : \text{常数}(0.04-0.06)$

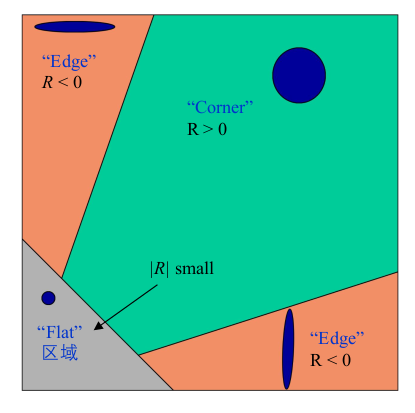
Harris角点检测步骤：

计算每个像素的局部梯度；
在每个像素周围的高斯窗口中计算二阶矩矩阵$M=\sum_{x,y}w(x,y)\begin{pmatrix}I_x^2&&I_xI_y\\I_xI_y&&I_y^2\end{pmatrix}$ ；
计算焦点响应函数$\mathcal{R}$ ；
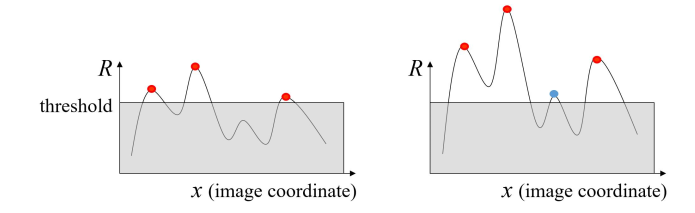
阈值过滤；
查找相应函数的局部最大值（非极大值抑制）。

角点性质：

对光照变化具有不变性；
对几何变化具有协不变性；
角点不具有尺度不变性；
对于亮度的仿射变化具有部分不变性：
- 计算过程中使用的是导数信息，因此，对于整体亮度变化具有不变性： $I\to I+b$ ；
- 对于亮度放缩，仅具有部分不变性： $I \to aI$。

2、局部特征：尺度不变区域检测

2.1、基础知识

尺度不变性：

目标：在不同尺度的图像中独立地检测出同一目标所占据的区域。
方法：需要设计尺度选择机制来寻找具有尺度不变性的特征区域。

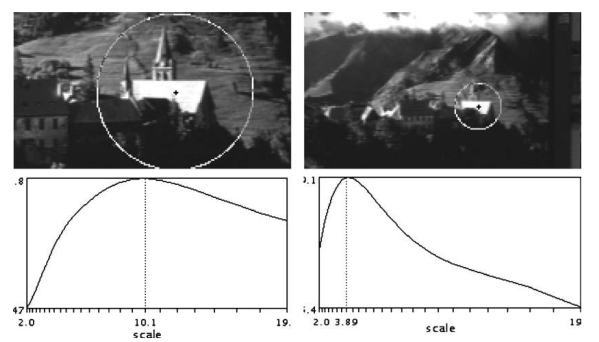
尺度匹配： 拉普拉斯算子尺度（标准差）与信号尺度“匹配”时，算子的响应幅值在尺度区域的中心达到最大。

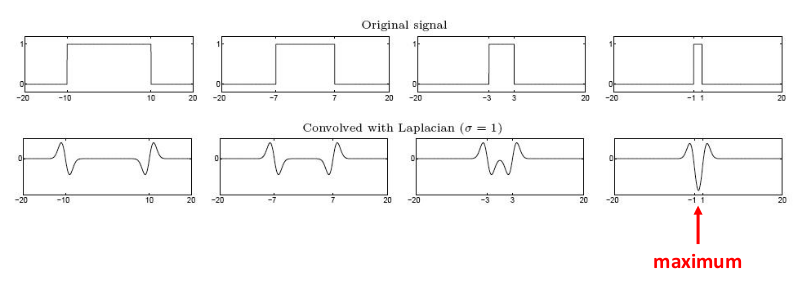
尺度选择：

目标：将输入信号与多个不同尺度（标准差）拉普拉斯算子卷积，通过最大响应确定信号的尺度。
存在问题：拉普拉斯相应强度随着尺度的增加而衰减。

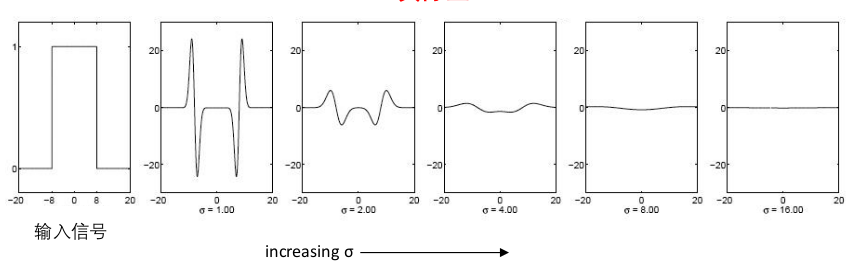
尺度归一化： 将卷积后的信号 乘以 $\sigma^2$ 来归一化响应强度。

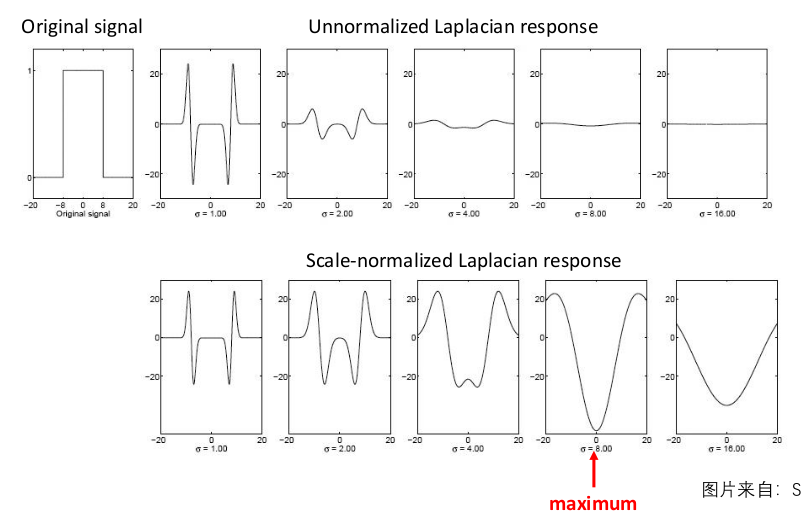
高斯拉普拉斯算子： 用于二维区域检测的圆形对称算子

$\nabla_{norm}^2g=\sigma^2\left(\frac{\partial^2g}{\partial x^2}+\frac{\partial^2g}{\partial y^2}\right)$

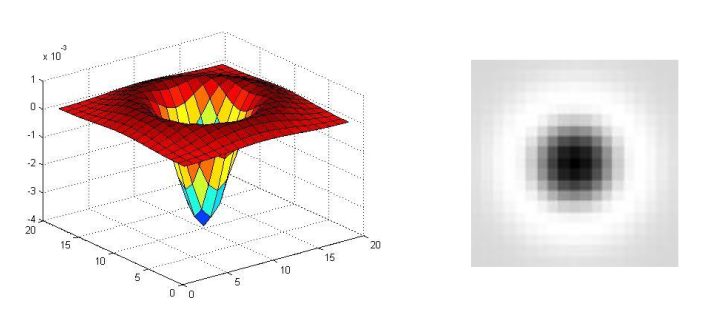
拉氏算子尺度（标准差）与信号半径 $r$ 之间的关系：

为获得最大响应，拉氏算子的零点必须与圆对齐。
拉是算子由$(x^{2}+y^{2}-2\sigma^{2})e^{-(x^{2}+y^{2})/2\sigma^{2}}$ 给出，最大响应发生在 $\sigma=r/\sqrt{2}$ 处。

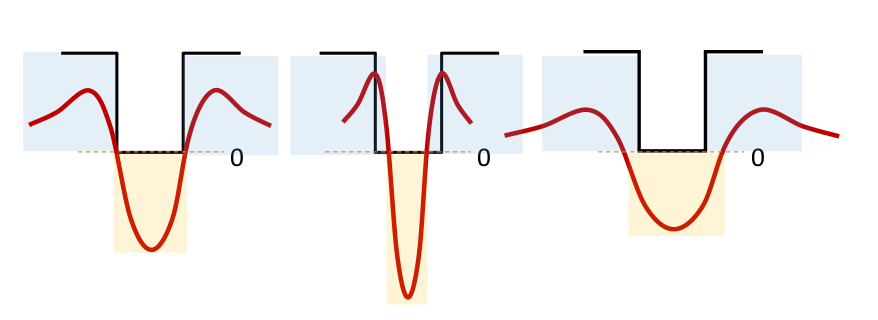
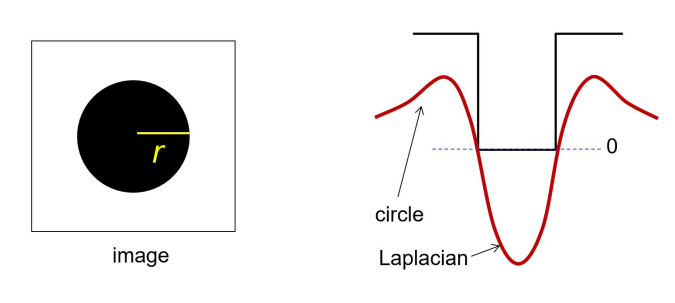
区域的尺度： 区域尺度定义为产生拉普拉斯响应峰值的尺度。

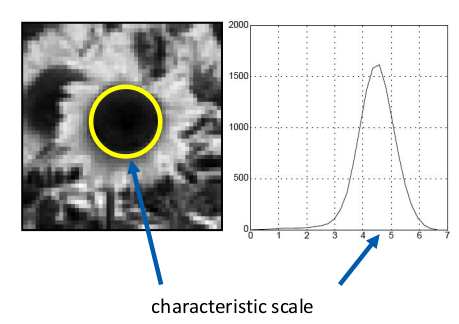
尺度不变区域检测检测器：

在多个尺度上使用归一化拉氏算子对图像进行卷积；
对于每个像素，在尺度空间中找到拉氏响应值的平方最大值。

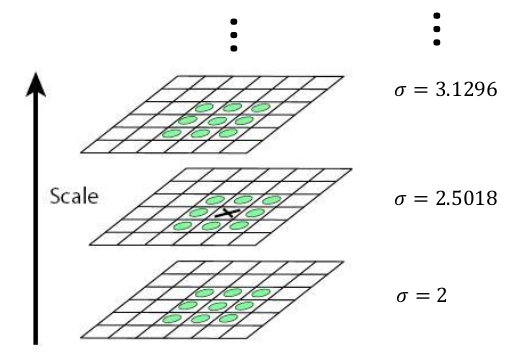
高效实现方法：

Harris-Laplacian：图像坐标空间中的 Harris 角点检测，尺度上采用拉氏算子。
SIFT：在空间和尺度上的高斯差分。

2.2、SIFT特征

DOG算子： 采用 DOG（差分高斯）近似逼近拉氏算子。

$\text{拉氏算子：}L=\sigma^{2}\left(G_{xx}(x,y,\sigma)+G_{yy}(x,y,\sigma)\right) \\ \text{高斯差分：}DoG=G(x,y,k\sigma)-G(x,y,\sigma) \\ \text{关系：} G(x,y,k\sigma)-G(x,y,\sigma)\approx(k-1)\sigma^2\nabla^2G$

SITF特性：

减少计算量：随着 $\sigma$ 增加，计算量成 $6\sigma+1$ 增加，且 $k>1$ ，导致计算量越来越大。DOG与原拉氏算子相差 $(k-1)$ ，能有效降低计算量。
提高效率：提取特征过程中不是一味提高 $\sigma$ ，而是对图像进行缩小后采用同样的 $\sigma$ 进行提取，提取后的特征按照图像缩小比例进行放大，得到原图提取的特征。

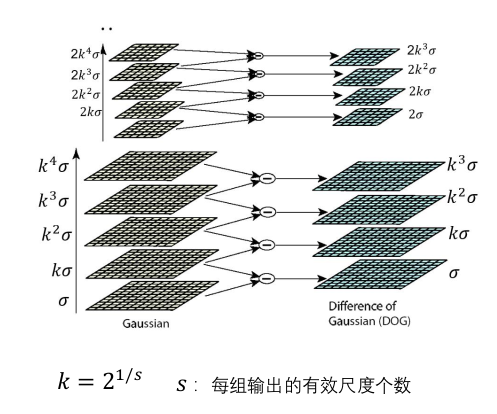
$s$ 取值： 一般取 $s=\sqrt{2}$ ，使得放缩成等比例的采样间隔。

SIFT特征文献： Distinctive Image Features from Scale-Invariant Keypoints

尺度归一化： 将对应的区域转换成相同大小的圆圈。

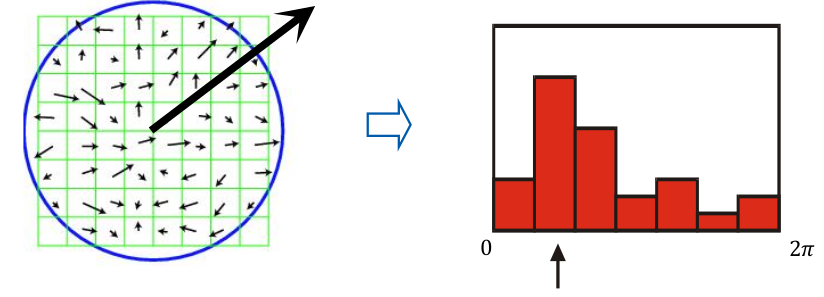
消除旋转歧义： 为图像窗口指定唯一方向：

创建局部区域的梯度方向直方图；
设置直方图峰值方向为主方向；
根据主方向对局部区域进行旋转。

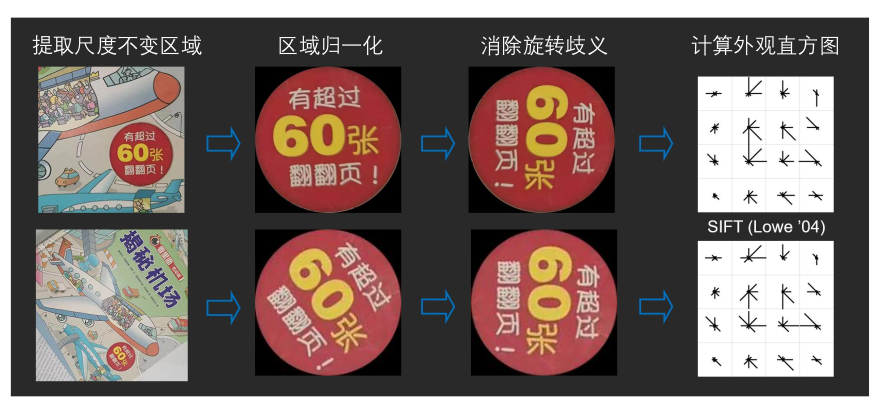
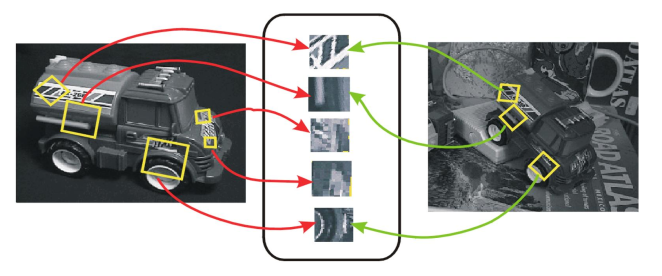
特征匹配： 对右图中的每个特征点 $i$ 在左图中：

找到距离其最近的特征点 $j_1$ 以及次近的特征点 $j_2$ ，并记录 $j_1,j_2$ 与特征点 $i$ 之间的距离为 $d_1,d_2$；
计算距离比 $d_1/d_2$ ，如果小于某个阈值，如0.6，则认为作图特征点 $i$ 与右图特征点 $j_1$ 是一对匹配点。

3、模型拟合之RANSAC

RANSAC： 随即采样一致性（Random sample consesus, RANSAC）：一种适用于数据受到异常值污染的模型拟合方法。

基本步骤：

随机均匀采样获取模型求解所需的最小子集；
应用该子集估计模型参数；
计算剩余样本与当前模型一致性，统计满足当前模型点（内点）的个数，作为当前模型分数；
以设定的次数重复上述步骤，最终输出分数最高的模型。

参数设置：

初始点数量 $s$ ：模型求解所需的最少的点的个数；
距离门线 $\tau$ ；
采样次数 $N$ ：选择采样次数 $N$ 使得至少有一次采样为真实解的概率为 $p$ （如： $p=0.99$）

$\begin{aligned}&(1-(1-e)^s)^N=1-p\\\\&N=\log{(1-p)}/\log{(1-(1-e)^s)}，\quad e \text{为外点率（噪点占全部点的比率）}\end{aligned}$

自适应迭代次数： 外点率通常是未知的，按最坏的情况估计，如 50%；然后，根据计算结果自适应调整外点比率，修正所需要的总采样次数。

$N = \infty,\text{采样次数}=0,e=1$ ；
While $N$ > 采样次数：
1. 采样一组样本点，计算模型内点数；
2. 设置 $e’=1-\text{内点数/总点数}$ ；
3. if ($e’<e$) 令 $e=e’$ ，基于 $e$ 计算所需的迭代次数 $N$ ；
4. 采样次数 + 1.

RANSAC 估计基础矩阵：

输入：左、右图像的所有匹配点对；
输出：两副图像间的基础矩阵 $F$ ：
1. 随机均匀采样八对匹配点对；
2. 基于采样点对，使用归一化八点法估计基础矩阵 $\hat{F}$；
3. 计算生于匹配点对是否满足当前 $\hat{F}$ ，统计满足当前 $\hat{F}$ 的匹配点对数量作为当前 $\hat{F}$ 分数；
4. 以设定的次数重复1-3 ；
5. 使用最高分数的 $\hat{F}$ 的所有匹配点对估计基础矩阵 $F$ ；
6. 输出 $F$ 。