SLAM导航实战（三）：SLAM——数学基础

前言

本系列主要基于《机器人SLAM导航——核心技术与实战》一书进行学习总结。

由于SLAM部分篇幅较长，且内容较为重要，预计按照作者章节安排从数学基础、激光SLAM、视觉SLAM、其他SLAM四个部分对其进行整理归纳。

简介

本章节作者通过介绍SLAM领域相关的数学基础部分，为后续SLAM算法的学习做好铺垫，具体数学推导笔者也会跟随作者在本篇总结做详细整理。

SLAM发展简史

最初，机器人的定位与建图是独立的两个问题，后续采用概率理论框架对机器人的不确定性进行讨论，同时把地图的位姿和地图路标做统一估计，才算是SLAM问题研究的起源。

SLAM也从基于滤波的古典时期过渡到现在基于优化方法的现代时期。

数据关联、收敛、一致性

数据关联：传感器数据与已构建数据进行匹配，闭环反馈就需要数据之间足够的关联性

收敛：系统数据的收敛性是理论上衡量系统的可行性的指标之一

一致性：分为强一致性和弱一致性，主要区别在于弱一致性是将偏差大的值的概率慢慢趋近于0，而强一致性是所有观测值在整个过程严格收敛于目标 $\theta$

SLAM基本理论

滤波方法：可以看成一种增量算法，获取每一时刻的信息，并将其分解至贝叶斯网络的概率分布来估计当前时刻的状态。

优化方法：不断累积获取到的信息，并基于此计算机器人轨迹及路标点。其计算信息存储在各个待估计变量间的约束中。通过近似线性化或者迭代的方法进行求解。

二者区别： 最大似然及最小二乘的区别，优化方法之间限制于存储的问题，在约束结构稀疏性的研究下得到了进一步的解决，从而占据当前SLAM研究的主导地位。

SLAM中的概率理论

机器人实际运行情况下存在传感器测量噪声、电机控制偏差、计算机软件计算精度近似等不确定性，故需要用概率对其不确定性进行描述估计。

单纯的运动会导致机器人系统整体的不确定性增大，引入观测可以使系统整体的不确定性降低。

状态估计问题

SLAM问题本质上属于状态估计问题，其估计观测的便是机器人的位姿以及路标点。

机器人系统运动过程中不断对路标点以及自身位姿进行估计，二者概率描述如下：

$P(z_k|x_k,m) \\ P(x_k|x_{k-1},u_k)$

SLAM问题解决的便是对于路标以及机器人位姿的估计问题。（注：SLAM的估计并不是简单的路标估计和位姿估计的乘积）

$P(x_k,m|Z_{0:k},U_{0:k},x_0)$

概率运动模型

速度运动模型

在不考虑速度误差的情况下，机器人的状态转移方程可以表示为：

$x_k=\begin{bmatrix} x' \\ y' \\ \theta ' \end{bmatrix} =g(x_{k-1},u_k)= \begin{bmatrix} x \\ y \\ \theta \end{bmatrix}+ \begin{bmatrix} cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} v_x \\ v_y \\ \omega _z \end{bmatrix} \Delta t$

上式需要满足两个条件：运动时间很小；实际前馈运动不存在误差

若此时考虑速度的误差，且$u_k、x_{k-1}、x_k$均服从高斯分布，此时$u_k$的协方差矩阵表示为：

$\sum u_k=\begin{bmatrix} \sigma_{v_x}^2 & 0 & 0\\ 0 & \sigma_{v_y}^2 & 0\\ 0 & 0 & \sigma_{w_z}^2 \end{bmatrix}$

由此，对状态转移函数进行一阶泰勒级数展开线性化后，计算$x_k$的协方差矩阵

$\sum x_k=\begin{bmatrix} \frac{\partial g}{\partial x_{k-1}} & \frac{\partial g}{\partial u_k}\\ \end{bmatrix} \begin{bmatrix} \sum x_{k-1} & 0_{3\times3}\\ 0_{3\times3} & \sum x_{u_k} \end{bmatrix} \begin{bmatrix} \frac{\partial g}{\partial x_{k-1}} & \frac{\partial g}{\partial u_k}\\ \end{bmatrix}^T$

同样的，上述模型也是基于两个前提条件：运动时间很小；运动以及状态估计误差服从高斯分布

里程计模型

由于速度运动模型条件假设过于严格，故主要采用实际工程更加可行的里程计模型

在考虑里程计误差，且变量服从高斯分布的情况下，其运动协方差表示为：

$\sum u_k=\begin{bmatrix} \sigma_{\Delta_x}^2 & 0 & 0 & 0 & 0 & 0\\ 0 & \sigma_{\Delta_y}^2 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & \sigma_{\Delta_\theta }^2 \end{bmatrix}$

上式表示机器人三维空间运动协方差矩阵，若机器人限制于二维平面，则由上式矩阵内形式表示，式中，各变量表示如下：

$\sigma_{\Delta_x}^2 = \xi_{\Delta xy} + \alpha_1 \sqrt[2]{(\Delta x)^2 + (\Delta y)^2} + \alpha_2 |\Delta \theta | \\ \sigma_{\Delta_y}^2 = \xi_{\Delta xy} + \alpha_1 \sqrt[2]{(\Delta x)^2 + (\Delta y)^2} + \alpha_2 |\Delta \theta | \\ \sigma_{\Delta_\theta}^2 = \xi_{\Delta \theta} + \alpha_3 \sqrt[2]{(\Delta x)^2 + (\Delta y)^2} + \alpha_4 |\Delta \theta |$

观察上式，里程计误差可以用底盘参数$\alpha_1 \sim \alpha_4$进行表示

误差直接设定为常数的理论依据：通常里程计数据是固定时间间隔发布，一定时间内的运动和旋转量基本一样

概率观测模型

传感器观测两步走：提取环境路标特征；数据关联

波束模型

这部分的误差假设不太明白，所以暂时跳过

概率图模型

图结构主要使得概率模型中的各个随机变量关系变得更加直观，也使复杂的概率计算过程得到简化

这部分主要使关于因子图内容，故对其他概念做简要概述

贝叶斯网络： 有向无环图，分为静态贝叶斯网络、动态贝叶斯网络 （注：SLAM中应用就是动态贝叶斯网络）

马尔可夫网络： 无向（有环）图，其中还涉及到团的概念

本质上都是应用贝叶斯准则对其分解为各部分条件独立的情况下的随机变量的乘积，再将这些“小”乘积用图的形式表达出来变量之间的关系

因子图

引入一个简单的SLAM模型

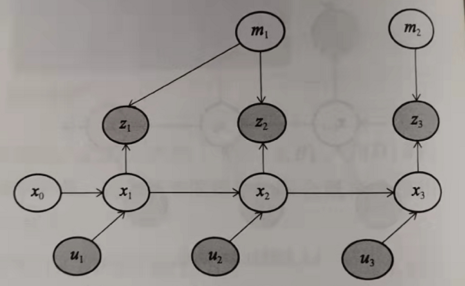
其各部分的联合概率分布表示如下：

$\begin{aligned} P(\boldsymbol{X}, \boldsymbol{m}, \boldsymbol{Z}, \boldsymbol{U})=&\left.\left.P\left(\boldsymbol{m}_{1}\right) P\left(\boldsymbol{m}_{2}\right) P\left(\boldsymbol{u}_{0}\right) P\left(\boldsymbol{u}_{1}\right) P\left(\boldsymbol{u}_{2}\right)\right\} \text { ( 先验, 可忽略) }\right) \times \\ &\left.\left.P\left(\boldsymbol{x}_{0}\right) P\left(\boldsymbol{x}_{1} \mid \boldsymbol{x}_{0}, \boldsymbol{u}_{1}\right) P\left(\boldsymbol{x}_{2} \mid \boldsymbol{x}_{1}, \boldsymbol{u}_{2}\right) P\left(\boldsymbol{x}_{3} \mid \boldsymbol{x}_{2}, \boldsymbol{u}_{3}\right)\right\} \text { (运动) }\right) \times \\ &\left.P\left(\boldsymbol{z}_{1} \mid \boldsymbol{x}_{1}, \boldsymbol{m}_{1}\right) P\left(\boldsymbol{z}_{2} \mid \boldsymbol{x}_{2}, \boldsymbol{m}_{1}\right) P\left(\boldsymbol{z}_{3} \mid \boldsymbol{x}_{3}, \boldsymbol{m}_{2}\right)\right\} \text { (观测) } \end{aligned}$

上式由先验（已知，可忽略）、运动、观测组成，由传感器获得的$U、Z$后对不可测量的$X、m$进行推理估计，一般采用最大后验估计

$S_{MAP}=arg \max_S P(S|V) \\ V=\{Z,U\} \\ S=\{X,m\}$

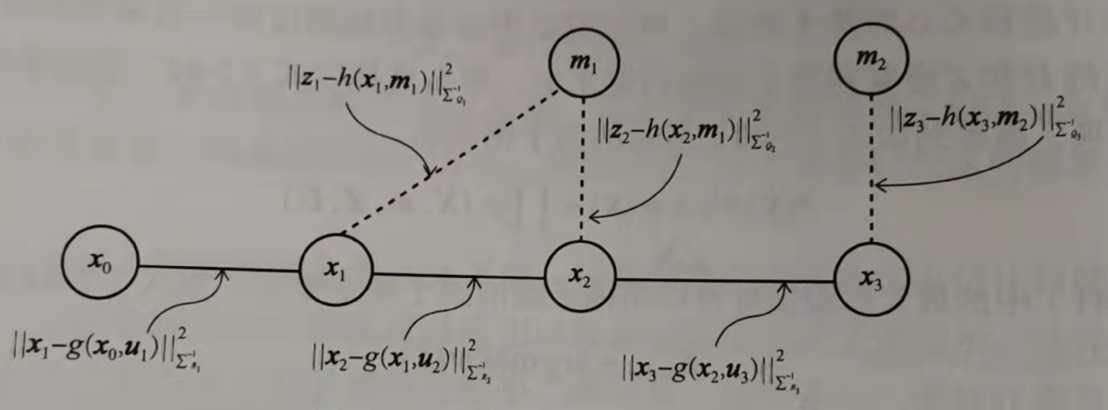
通过构建运动和观测两个约束构建因子函数

$P(\boldsymbol{S} \mid \boldsymbol{V}) \propto \psi(\boldsymbol{S})=\prod \psi_{i}(\boldsymbol{X}, \boldsymbol{m}, \boldsymbol{Z}, \boldsymbol{U})$

改写最大后验估计为

$S_{MAP}=arg \max_S \psi(\boldsymbol{S})$

引入噪声，且噪声符合高斯分布，得到运动和观测的噪声模型

$\begin{array}{l} \boldsymbol{x}_{k}=g\left(\boldsymbol{x}_{k-1}, \boldsymbol{u}_{k}\right)+\boldsymbol{R}_{k} \\ \boldsymbol{z}_{k}=h\left(\boldsymbol{x}_{k}, \boldsymbol{m}_{j}\right)+\boldsymbol{Q}_{k} \end{array}$

用运动误差及观测误差构造两种因子项

$\begin{array}{l} \psi_{i 1}\left(\boldsymbol{x}_{k}, \boldsymbol{x}_{k-1}\right) \propto \mathrm{e}^{-\frac{1}{2}\left(x_{k}-g\left(x_{k-1}, u_{k}\right)\right)^{\mathrm{T}} \Sigma_{R_{k}}^{-1}\left(x_{k}-g\left(x_{k-1}, u_{k}\right)\right)} \\ \psi_{i 2}\left(\boldsymbol{x}_{k}, \boldsymbol{m}_{j}\right) \propto \mathrm{e}^{-\frac{1}{2}\left(z_{k}-h\left(x_{k}, m_{j}\right)\right)^{\mathrm{T}} \Sigma_{Q_{k}}^{-1}\left(z_{k}-h\left(x_{k}, m_{j}\right)\right)} \end{array}$

整理后得到

$\psi(\boldsymbol{S}) \propto \prod_{i 1} \psi_{i 1}\left(\boldsymbol{x}_{k}, \boldsymbol{x}_{k-1}\right) \cdot \prod_{i 2} \psi_{i 2}\left(\boldsymbol{x}_{k}, \boldsymbol{m}_{j}\right)$ $\begin{aligned} \boldsymbol{S}_{\mathrm{MAP}}=& \arg \max _{s} \psi(\boldsymbol{S}) \\ \propto &\left.\arg \max _{s}\left(\sum_{i 1} \ln \psi_{i 1}\left(\boldsymbol{x}_{k}, \boldsymbol{x}_{k-1}\right)+\sum_{i 2} \ln \psi_{i 2}\left(\boldsymbol{x}_{k}, \boldsymbol{m}_{j}\right)\right)\right) \\ \propto & \arg \max _{s}\left(-\frac{1}{2} \sum_{i 1}\left(\boldsymbol{x}_{k}-g\left(\boldsymbol{x}_{k-1}, \boldsymbol{u}_{k}\right)\right)^{\mathrm{T}} \boldsymbol{\Sigma}_{\boldsymbol{R}_{k}}^{-1}\left(\boldsymbol{x}_{k}-g\left(\boldsymbol{x}_{k-1}, \boldsymbol{u}_{k}\right)\right)-\right.\\ &\left.\frac{1}{2} \sum_{i 2}\left(\boldsymbol{z}_{k}-h\left(\boldsymbol{x}_{k}, \boldsymbol{m}_{j}\right)\right)^{\mathrm{T}} \boldsymbol{\Sigma}_{\boldsymbol{Q}_{k}}^{-1}\left(\boldsymbol{z}_{k}-h\left(\boldsymbol{x}_{k}, \boldsymbol{m}_{j}\right)\right)\right) \\ \propto &\left.\arg \min _{s}\left(\sum_{i 1}\left\|\boldsymbol{x}_{k}-g\left(\boldsymbol{x}_{k-1}, \boldsymbol{u}_{k}\right)\right\|_{\Sigma_{k_{k}}^{-1}}^{2}+\sum_{i 2}\left\|\boldsymbol{z}_{k}-h\left(\boldsymbol{x}_{k}, \boldsymbol{m}_{j}\right)\right\|_{\Sigma_{\ell_{k}}^{-1}}\right)^{2}\right) \end{aligned}$

（引入对数，将乘法转化为加法）

由上式可得，0均值高斯噪声SLAM问题采用最大后验估计等于最小二乘估计。其实满足0均值高斯噪声，最大后验等价最小均方误差等于最小二乘，因子图应用到SLAM问题，对滤波方法转向优化方法起到关键作用

SLAM中的估计理论

研究问题过程中，对某个参数感兴趣但却无法准确获得，，只能通过一组观测的样本值对猜测参数，这便是估计。

估计量的性质

一致性
偏差性

估计量的构建

最好的估计应该为最小方差无偏估计（MVUE），但其实现往往较难，故通常寻找近似方法。本书中作者介绍常用的近似方法总体下来构建思路大同小异，再次不一一描述，而是简要总结其构建步骤及各近似方法之间的联系。

构建过程通常如下：

构建代价函数
对代价函数进行求导，并领倒数等于0，求出代价函数极值点

经典估计有：最大似然估计、最小二乘估计

“动态”估计有：贝叶斯估计 （注：动态估计是笔者自己瞎取的，因为估计值设定为可变，不确定，故称为动态）

各估计的关系

此处直接引用作者的两张图做整理，直接总结了本小节的核心内容

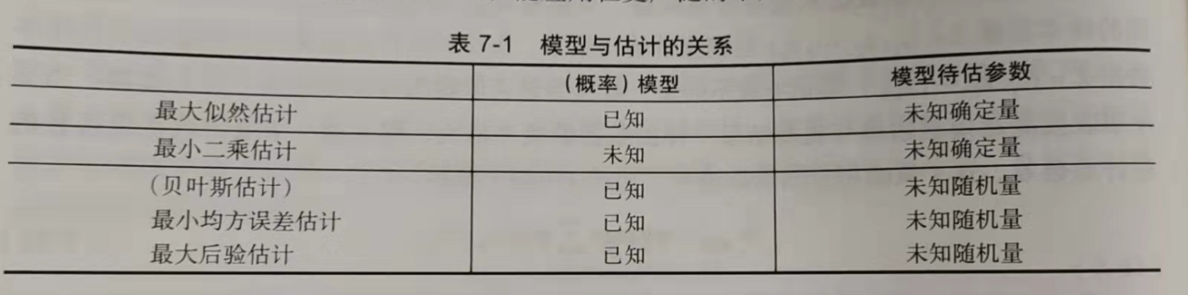
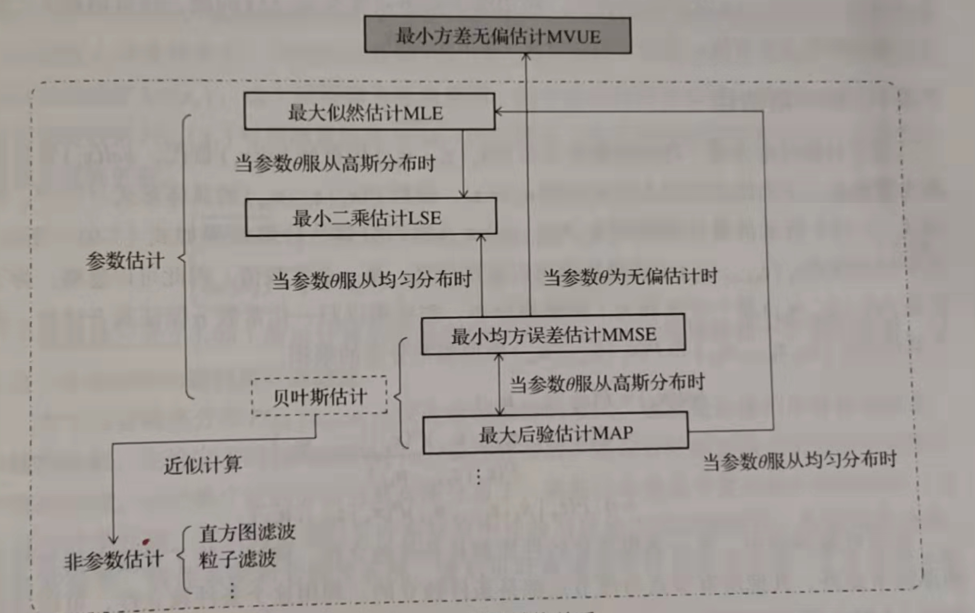
基于贝叶斯网络的状态估计

该部分主要是滤波算法的介绍，后续专门整理，故先跳过

基于因子图的状态估计

贝叶斯网络中的最大后验估计等效于因子图中的最小二乘估计

对于最小二乘估计通常有两个解法：线性近似处理；迭代求解

直接求解法

主要是采用了Cholesky；QR两种分解方法对方程进行求解

优化方法

梯度下降法

$\begin{array}{l} \operatorname{do}\left\{x^{(k+1)}=x^{(k)}-\alpha \cdot \nabla \psi\left(x^{(k)}\right)\right. \\ \} \text { while }\left(\psi\left(x^{(k+1)}\right)<\psi\left(x^{(k)}\right)\right) \end{array}$

沿梯度方向不断逼近目标点，但迭代过程中步长不变使得其可能出现迭代次数过多（步长太小）；目标点附近震荡（步长太长）的问题

机器人应用迭代法时，需要对机器人的空间位姿 pose 进行求导，但其内部存在的额外约束导致求导和求和运算无法直接进行，此时就需要将其转换到李代数上进行求导和求和操作。

最速下降法

$\alpha_{k}=\arg \min _{\alpha \geqslant 0} \psi\left(\boldsymbol{x}^{(k)}-\alpha \cdot \nabla \psi\left(\boldsymbol{x}^{(k)}\right)\right)$

为解决梯度下降的问题，采用可变步长的方法，通常步长方向取垂直于两端梯度等高线的方向

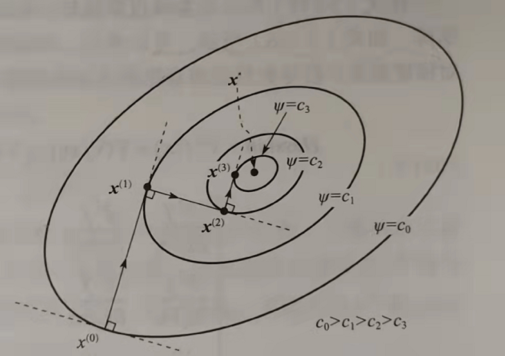
高斯-牛顿法

几个概念：

梯度：多维自变量与一维因变量函数中，函数的一阶导数
海森矩阵：多维自变量与一维因变量函数中，函数的二阶导数
雅可比矩阵：多维自变量与多维因变量函数中，函数的一阶导数
多个海森矩阵组合：多维自变量与多维自变量函数中，函数的二阶导数

由于需要对某一点自变量做二次泰勒展开，故需要求其梯度和海森矩阵

$\psi(x)=\sum_{i}\left\|\boldsymbol{y}_{i}-f\left(\boldsymbol{x}_{i}\right)\right\|_{\Sigma_{i}^{-1}}^{2}=\sum_{i=1}^{m}\left\|e_{i}(\boldsymbol{x})\right\|^{2}=\|e(\boldsymbol{x})\|^{2}=e(\boldsymbol{x})^{\mathrm{T}} \cdot e(\boldsymbol{x})$

梯度和海森矩阵分别为

$\underbrace{\nabla \psi}_{g r a d_{\psi}}=2 \cdot \text { Jacobian }_{e}^{\mathrm{T}} \cdot e(\boldsymbol{x}) \\ \underbrace{\nabla^{2} \psi(x)}_{\text {Hessian }_{\psi}} \approx 2 \cdot \text { Jacobian }_{e}^{\mathrm{T}} \cdot \text { Jacobian }_{e}$

代入代价函数

$\begin{aligned} \nabla \psi(\boldsymbol{x}) & \approx \nabla\left(\psi\left(\boldsymbol{x}^{(k)}\right)+\left(\boldsymbol{x}-\boldsymbol{x}^{(k)}\right)^{\mathrm{T}} \cdot \nabla \psi\left(\boldsymbol{x}^{(k)}\right)+\frac{1}{2}\left(\boldsymbol{x}-\boldsymbol{x}^{(k)}\right)^{\mathrm{T}} \cdot \nabla^{2} \psi\left(\boldsymbol{x}^{(k)}\right) \cdot\left(\boldsymbol{x}-\boldsymbol{x}^{(k)}\right)\right) \\ &=\nabla \psi\left(\boldsymbol{x}^{(k)}\right)+\nabla^{2} \psi\left(\boldsymbol{x}^{(k)}\right) \cdot\left(\boldsymbol{x}-\boldsymbol{x}^{(k)}\right)=0 \\ & \Leftrightarrow 2 \cdot \boldsymbol{J a c o b i a n}_{e}^{\mathrm{T}} \cdot e\left(\boldsymbol{x}^{(k)}\right)+2 \cdot \boldsymbol{J a c o b i a n}_{e}{ }^{\mathrm{T}} \cdot \boldsymbol{J a c o b i a n}_{e} \cdot\left(\boldsymbol{x}-\boldsymbol{x}^{(k)}\right)=0 \\ \text { 令 } \Delta \boldsymbol{x}=\boldsymbol{x}-\boldsymbol{x}^{(k)}, & \text { 那么: } \boldsymbol{J}_{e}^{\mathrm{T}} \boldsymbol{J}_{e} \cdot \Delta \boldsymbol{x}=-\boldsymbol{J}_{e}^{\mathrm{T}} \cdot \boldsymbol{e} 。 \end{aligned}$

则此时下一个迭代点为

$\boldsymbol{x}^{(k+1)}=\boldsymbol{x}^{(k)}-\left(\boldsymbol{J}_{e\left(\boldsymbol{x}^{(k)}\right)}{ }^{\mathrm{T}} \boldsymbol{J}_{e\left(\boldsymbol{x}^{(k)}\right)}\right)^{-1} \cdot \boldsymbol{J}_{e\left(\boldsymbol{x}^{(k)}\right)}{ }^{\mathrm{T}} \cdot e\left(\boldsymbol{x}^{(k)}\right)$

其中雅可比的转置与自身的乘积采用Cholesky；QR求解

列文伯格-马夸尔特算法

高斯-牛顿法只能在目标点附近有较好的效果，且不一定能向目标点方向迭代

$\left(\boldsymbol{J}_{e}^{\mathrm{T}} \boldsymbol{J}_{e}+\mu_{k} \cdot \boldsymbol{I}\right) \cdot \Delta \boldsymbol{x}=-\boldsymbol{J}_{e}^{\mathrm{T}} \cdot \boldsymbol{e} \\ \Delta \boldsymbol{x}=-\left(\boldsymbol{J}_{e}^{\mathrm{T}} \boldsymbol{J}_{e}+\mu_{k} \cdot \boldsymbol{I}\right)^{-1} \cdot \boldsymbol{J}_{e}^{\mathrm{T}} \cdot \boldsymbol{e}$

本质上引入了$u_k$这个阻尼系数，其取值取决于如下比值

$\begin{array}{c} \Delta \psi=\psi\left(\boldsymbol{x}^{(k)}+\Delta \boldsymbol{x}\right)-\psi\left(\boldsymbol{x}^{(k)}\right)=\psi\left(\boldsymbol{x}^{(k+1)}\right)-\psi\left(\boldsymbol{x}^{(k)}\right) \\ \Delta \varphi=\varphi(\Delta \boldsymbol{x})-\varphi(\boldsymbol{0})=2 \Delta \boldsymbol{x}^{\mathrm{T}} \cdot \boldsymbol{J}_{e}^{\mathrm{T}} \cdot \boldsymbol{e}+\Delta \boldsymbol{x}^{\mathrm{T}} \cdot \boldsymbol{J}_{e}^{\mathrm{T}} \cdot \boldsymbol{J}_{e} \cdot \Delta \boldsymbol{x} \end{array} \\$ $\gamma_{k}=\frac{\Delta \psi}{\Delta \varphi}=\frac{\psi\left(\boldsymbol{x}^{(k+1)}\right)-\psi\left(\boldsymbol{x}^{(k)}\right)}{2 \Delta \boldsymbol{x}^{\mathrm{T}} \cdot \boldsymbol{J}_{e}^{\mathrm{T}} \cdot \boldsymbol{e}+\Delta \boldsymbol{x}^{\mathrm{T}} \cdot \boldsymbol{J}_{e}^{\mathrm{T}} \cdot \boldsymbol{J}_{e} \cdot \Delta \boldsymbol{x}}$

通过$\gamma_{k}$来调节$\mu_{k}$：趋近1，高斯-牛顿主导；逼近0，梯度下降主导；比值小于0，则拒绝迭代，修改阻尼系数。

狗腿算法

列文伯格-马夸尔特算法存在拒绝迭代而浪费算力的情况

$\begin{array}{c} \Delta \boldsymbol{x}_{\mathrm{SD}}=-\alpha_{k} \cdot \nabla \psi\left(\boldsymbol{x}^{(k)}\right)=-\alpha_{k} \cdot 2 \cdot \boldsymbol{J a c o b i a n}_{e}^{\mathrm{T}} \cdot e\left(\boldsymbol{x}^{(k)}\right) \\ \Delta \boldsymbol{x}_{\mathrm{GN}}=-\left(\boldsymbol{J}_{e}^{\mathrm{T}} \boldsymbol{J}_{e}\right)^{-1} \cdot \boldsymbol{J}_{e}^{\mathrm{T}} \cdot \boldsymbol{e} \end{array}$

根据上述两个变量对阻尼系数进行调整，具体调整方式，参考下图

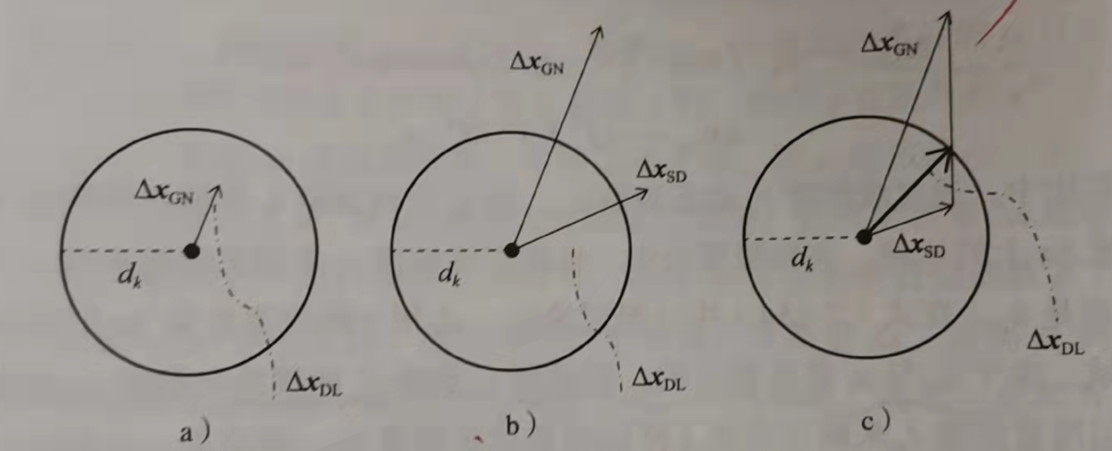
小结

可以清楚发现，每一种算法都是为了解决上面算法的问题作出的改进，理论上，算法不断优化，效果不断提升，但同时，其对算力的要求也不断增加，故需要根据实际情况选择对应的算法。

常用优化工具

g2o（轻量，所需依赖少）
ceres-Slover（数值自动求导，避免复杂雅可比计算）
GTSAM（优化过程能增量计算，优化速度快）

基本用法

图结构定义非线性最小二乘，定义状态量，约束关系
选用优化策略
启动求解器迭代

AppZ99's Blog