Dr_CAN课程学习——工程数学基础

前言

基于B站UP主DR_CAN视频所作的总结笔记

视频链接：DR_CAN——工程数学基础

特征值与特征向量

定义

对于一个给定的线性变换 $A$ ，它的特征向量 $v$ 经过这个线性变换的作用后，得到的新向量仍然与原来的 $v$ 保持在同一直线上，但其长度或方向或许会改变，即：

$Av = \lambda v$

其中 $\lambda$ 为标量，即特征向量的长度在该线性变换下缩放的比例，称为其特征值。

$e.g.$

将线性变换矩阵 $A$ 分别与向量 $v_1、v_2$ 相乘，看变换后向量是否与原向量保持同一直线上。

$A= \begin{pmatrix} 1 & 1 \\ 4 & -2 \\ \end{pmatrix} 、 v_1 = \begin{pmatrix} 1 \\ 2 \\ \end{pmatrix}、 v_2 = \begin{pmatrix} 1 \\ 1 \\ \end{pmatrix}$

可以发现 $v_2$ 在 $A$ 的作用下变换成 $2v_2$ 故满足其上述定义。

求解特征值、特征向量

$Av = \lambda v \\ Av - \lambda v = 0 \\ (A - \lambda I)v = 0 (\ast)\\ |A - \lambda I| = 0$

注：上式中 $(\ast)$式需要有非零解，则其行列式需为零

应用

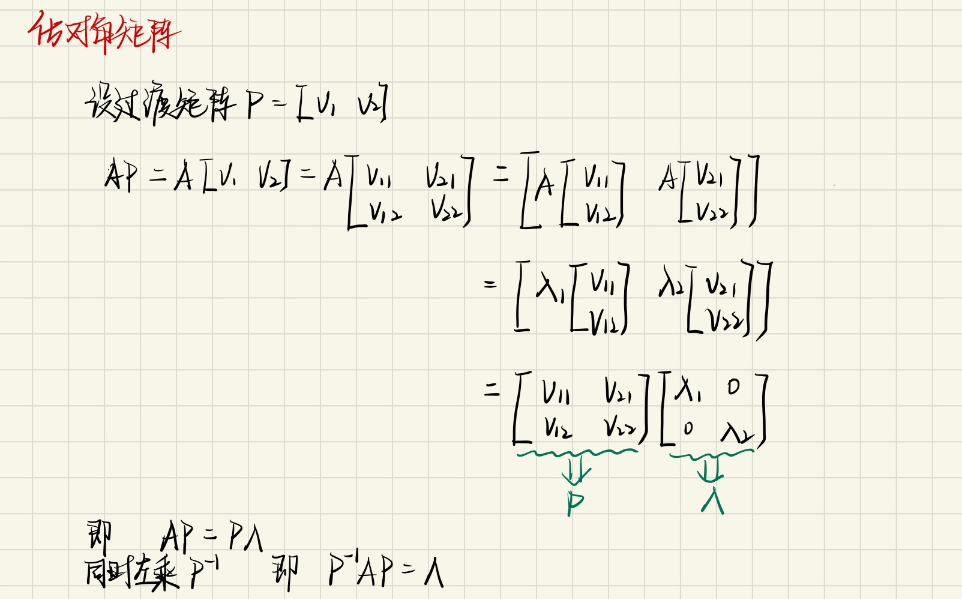
化对角矩阵

解耦

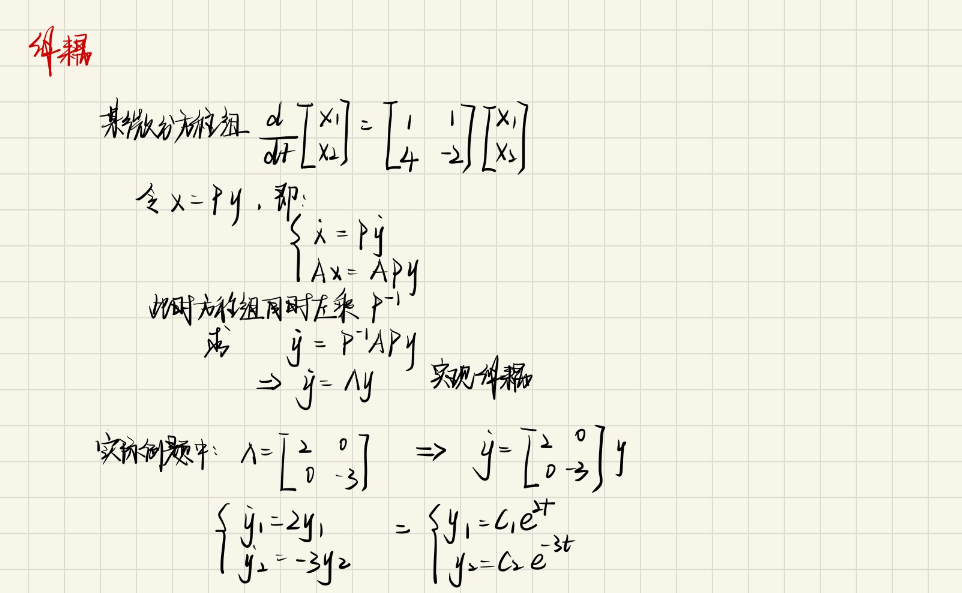
小结

加深了对于特征向量、特征值的理解
重温了特征值求解方法
理解了对角化公式的由来
理解了对角化在解耦过程中的应用

线性化、泰勒级数、泰勒公式

线性系统

条件：满足叠加原理

$x_1、x_2$ 为系统方程的解
$x_3 = k_1 x_1 + k_2 x_2$ （$k_1、k_2$ 为常数）
$x_3$ 为系统方程的解

泰勒级数

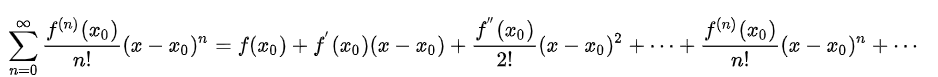
线性化

小结

卷积含义、LTI的冲激响应及卷积

LTI System

满足叠加原理、时不变原理的系统称为线性时不变系统。

LTI 中拉普拉斯变换与卷积的关系

系统表达

$F(s)H(s)=X(s)$

进行拉氏逆变换后，等于系统时域上输出与传函的卷积

$f(t)\ast h(t) = x(t)$

LTI 中冲激响应

根据 LTI 的叠加性质，任意的输出可以视为多个冲激响应的叠加

时间 $t$ 为第$i$ 个时刻冲激响应时间$i\Delta_T$，则系统输出：

$X(t) = \sum_{i=0}^i \Delta_Tf(i\Delta_T)h_\Delta(t - i\Delta_T)$

将$\Delta_T$ 趋向0取极限，则$\Delta_T = d\tau, i\Delta_T=\tau$

则此时有输出函数：

$X(t) = \int_0^t f(\tau)h(t-\tau)d\tau \\ 即:X(t)=f(t)\ast h(t)$

小结

根据本节的内容，其实任意的LTI 系统都可以由一系列的冲激响应去定义整个系统。那么如果我们在一个LTI 系统下输入一段信号并与一种近似冲激响应的信号做卷积处理，就可以理解为——我们把输入信号放在了对应的冲激响应的系统中。（注：这部分MATLAB实践放在后续章节中去分析）

思考过程：连续的输入信号切割成每一个单位冲激响应与某一时刻输入信号大小的乘积，即$t$ 时刻的输入可以看作是$\Delta_Tf(t)$ 大小的单位冲击响应，然后根据LTI 系统的叠加原理，将$t$ 时刻前的所有输入响应进行叠加，即可得到$t$ 时刻的输出信号，$\Delta_T$ 去极限就是积分，也就得到最终的卷积形式。

视频最后的例子的理解：每一时刻说话的声音由一个个浴室帘后声音的冲激响应叠加组成，其冲激响应特点是沉闷的回声，所有进行卷积后得到了人躲在浴室帘后说话的感觉。

欧拉公式证明

卷积的拉普拉斯变换

Sinx = 2 的证明

复数的三种表示

一般型

$z = a + bi$

三角型

$z = |z|cos(\theta) +|z|sin(\theta)i$

指数型

$z = |z|e^{i\theta}$

欧拉恒等式

当$\theta = \pi$ ，$|z|=1$有：

$e^{i\pi} + 1 = 0$

小结

通过数形转换的方式，加深对这三种形式的理解

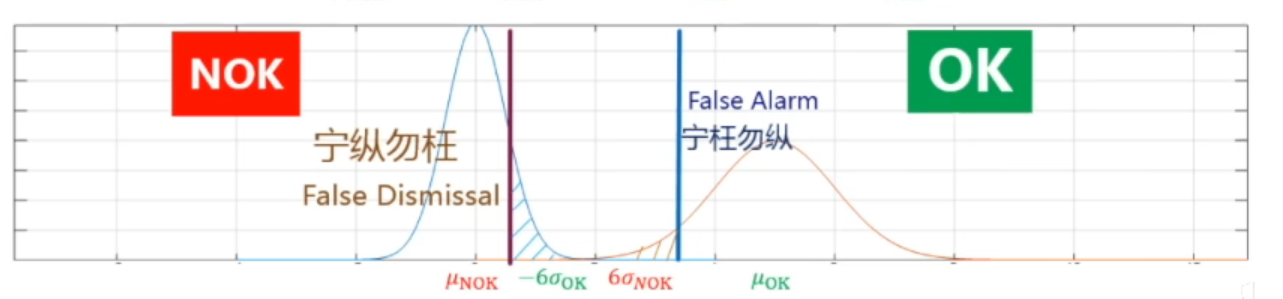
如何选取阈值

Six Sigma 选取原则

工业生产中，对于产品的品质把控一般采用Six Sigma的原则。

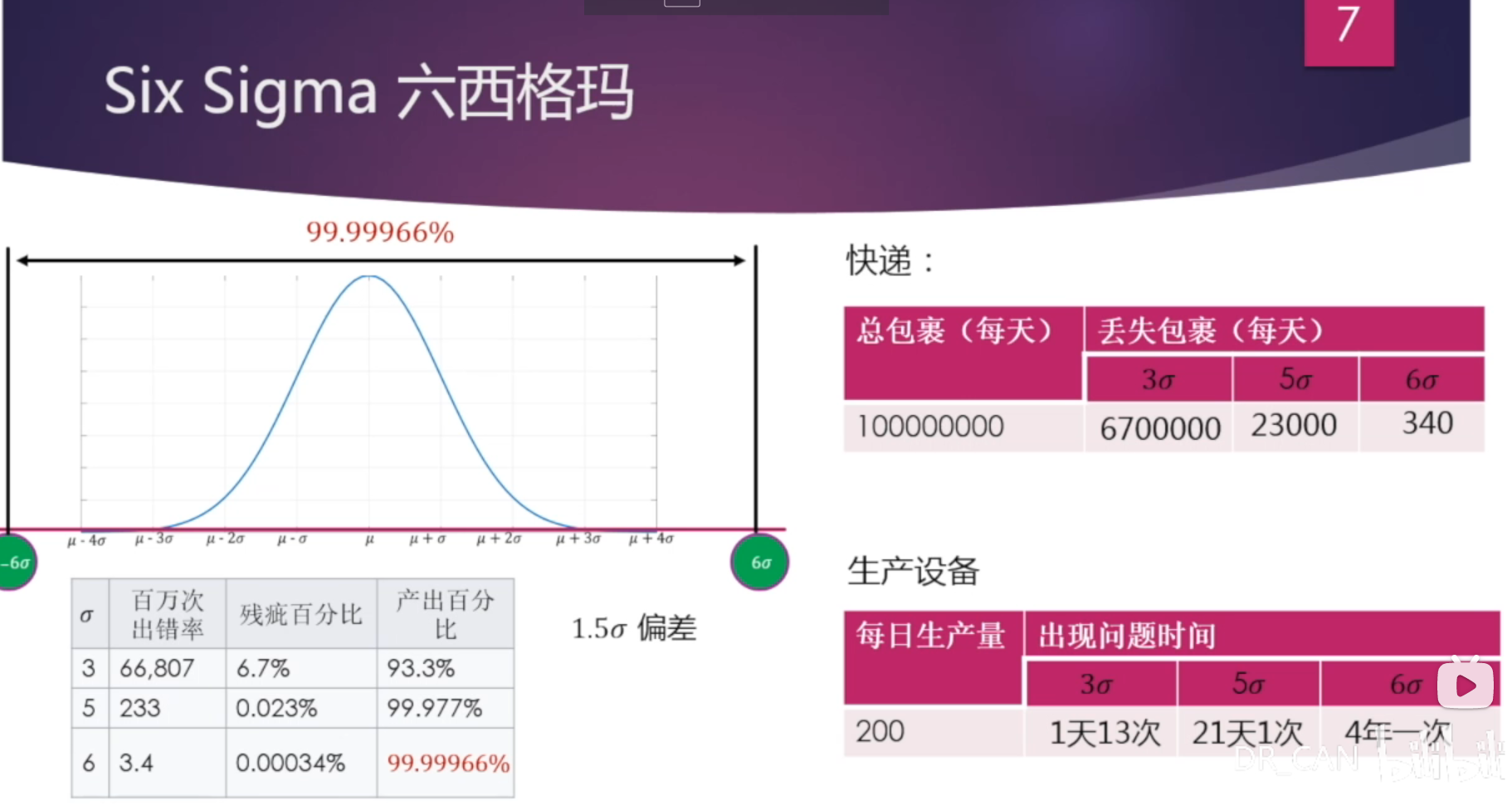
工程选择两种准则

当合格与不合格的Six Sigma存在重叠部分，那么根据实际情况选择宁纵无枉还是宁枉无纵